„Magnetosztatika példák - Eltolási áramsűrűség szolenoidban” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
(→Megoldás) |
||
| 21. sor: | 21. sor: | ||
Ebből pedig: | Ebből pedig: | ||
$$E = -\frac{1}{2}\mu_0 I_0 \omega r n \cos\left(\omega t \right)$$ | $$E = -\frac{1}{2}\mu_0 I_0 \omega r n \cos\left(\omega t \right)$$ | ||
| − | Így az elektromos eltolás és az eltolási | + | Így az elektromos eltolás és az eltolási áramsűrűség nagysága: |
$$D = -\frac{1}{2}\mu_0 \epsilon_0 I_0 \omega r n \cos\left(\omega t \right)$$ | $$D = -\frac{1}{2}\mu_0 \epsilon_0 I_0 \omega r n \cos\left(\omega t \right)$$ | ||
$$\frac{\partial D}{\partial t}= \frac{1}{2}\mu_0 \epsilon_0 I_0 \omega^2 r n \sin\left(\omega t \right)$$ | $$\frac{\partial D}{\partial t}= \frac{1}{2}\mu_0 \epsilon_0 I_0 \omega^2 r n \sin\left(\omega t \right)$$ | ||
</noinclude> | </noinclude> | ||
A lap 2013. október 1., 15:03-kori változata
Feladat
- Hosszú, egyenes szolenoid hosszegységenként
menettel rendelkezik, és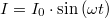 
erősségű váltakozó áram járja át. Határozzuk meg az eltolási áramsűrűséget a szolenoid tengelyétől mért távolság függvényében, ha szolenoid keresztmetszetének sugara 
!
Megoldás
A szolenoid belsejében változik a mágneses tér fluxusa, ezért ott örvényes elektromos tér indukálódik.
Írjuk fel a második Maxwell egyenletet egy 
sugarú gyűrűre, melynek tengelye egybe esik a szolenoid tengelyével:
![\[\oint \vec{E}\cdot \vec{dl} = -\frac{\partial}{\partial t} \iint \vec{B}\cdot \vec{dA}\]](/images/math/9/2/4/9243f81a00e331a33b95fa2fe072a9d4.png)
![\[E2\pi r = -\frac{\partial}{\partial t} B(t) r^2 \pi = -\frac{\partial}{\partial t} \mu_0 I_0\cdot \sin\left(\omega t\right) n r^2 \pi\]](/images/math/d/4/c/d4cf291e1f9626d5ff2888f61160fe6e.png)
Ebből pedig:
![\[E = -\frac{1}{2}\mu_0 I_0 \omega r n \cos\left(\omega t \right)\]](/images/math/a/a/8/aa8bff0156c6de783144c7b02f7fba86.png)
Így az elektromos eltolás és az eltolási áramsűrűség nagysága:
![\[D = -\frac{1}{2}\mu_0 \epsilon_0 I_0 \omega r n \cos\left(\omega t \right)\]](/images/math/9/2/6/926a523d1b9e0b2ce24cd0d136b5535f.png)
![\[\frac{\partial D}{\partial t}= \frac{1}{2}\mu_0 \epsilon_0 I_0 \omega^2 r n \sin\left(\omega t \right)\]](/images/math/0/8/b/08b7cf958b52b50fad02493e6c45ec19.png)
