„Munka, energia - 2.2.9” változatai közötti eltérés
A Fizipedia wikiből
a (→Feladat) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (2.2.9) Egy $\alpha=30^\circ$-os hajlásszögű lejtőre húzunk fel egy $m=5\,\mathrm{kg}$ tömegű testet, a lejtő hosszával párhuzamos erővel, állandó $P=150 \,\mathrm{W}$ teljesítménnyel. A mozgás végig egyenletes. Milyen magasra jut fel a test $\Delta t=5\,\mathrm{s}$ alatt? Mekkora a hatásfok? A lejtő és a test közötti súrlódási együttható $\mu=0,2$. | + | </noinclude><wlatex># (*2.2.9) Egy $\alpha=30^\circ$-os hajlásszögű lejtőre húzunk fel egy $m=5\,\mathrm{kg}$ tömegű testet, a lejtő hosszával párhuzamos erővel, állandó $P=150 \,\mathrm{W}$ teljesítménnyel. A mozgás végig egyenletes. Milyen magasra jut fel a test $\Delta t=5\,\mathrm{s}$ alatt? Mekkora a hatásfok? A lejtő és a test közötti súrlódási együttható $\mu=0,2$. |
</wlatex><includeonly><wlatex>{{Útmutatás|content= Egyenletes mozgásnál használható $P=Fv$.}}{{Végeredmény|content=$\eta=0,74$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content= Egyenletes mozgásnál használható $P=Fv$.}}{{Végeredmény|content=$\eta=0,74$}}</wlatex></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>#: Egyenletes mozgás esetén a lejtőre merőleges és a lejtővel párhuzamos erők is kiegyenlítik egymást. A lejtőre merőleges erők $$N=mg\cos\alpha\,,$$ ahol $N$ a nyomóerő. A lejtővel párhuzamos erők $$F=mg\sin\alpha+\mu N\,,$$ ahol $F$ az általunk kifejtett erő. Egyenletes mozgásnál $P=Fv$, így a test sebessége $$v=\frac{P}{F}=\frac{P}{mg(\sin\alpha+\mu\cos\alpha)}\,.$$ A test tehát $\Delta t$ idő alatt $d=v\Delta t$ utat tesz meg, amely alapján a test emelkedése $$h=d\sin\alpha= \frac{P \Delta t}{mg(1+\mu\,\mbox{ctg}\,\alpha)}=11,14\,\mathrm{m}\,.$$ A hasznos energia nyeresége a testnek a nyert helyzeti energiája $E_{h}=mgh$, míg a teljes általunk végzett munka $W=P\Delta t$. A hatásfok tehát $$\eta=\frac{E_{h}}{W}=\frac{1}{1+\mu\,\mbox{ctg}\,\alpha}=0,74\,.$$ | <wlatex>#: Egyenletes mozgás esetén a lejtőre merőleges és a lejtővel párhuzamos erők is kiegyenlítik egymást. A lejtőre merőleges erők $$N=mg\cos\alpha\,,$$ ahol $N$ a nyomóerő. A lejtővel párhuzamos erők $$F=mg\sin\alpha+\mu N\,,$$ ahol $F$ az általunk kifejtett erő. Egyenletes mozgásnál $P=Fv$, így a test sebessége $$v=\frac{P}{F}=\frac{P}{mg(\sin\alpha+\mu\cos\alpha)}\,.$$ A test tehát $\Delta t$ idő alatt $d=v\Delta t$ utat tesz meg, amely alapján a test emelkedése $$h=d\sin\alpha= \frac{P \Delta t}{mg(1+\mu\,\mbox{ctg}\,\alpha)}=11,14\,\mathrm{m}\,.$$ A hasznos energia nyeresége a testnek a nyert helyzeti energiája $E_{h}=mgh$, míg a teljes általunk végzett munka $W=P\Delta t$. A hatásfok tehát $$\eta=\frac{E_{h}}{W}=\frac{1}{1+\mu\,\mbox{ctg}\,\alpha}=0,74\,.$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. január 9., 15:34-kori változata
Feladat
- (*2.2.9) Egy
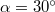-os hajlásszögű lejtőre húzunk fel egy 
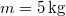tömegű testet, a lejtő hosszával párhuzamos erővel, állandó 
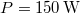teljesítménnyel. A mozgás végig egyenletes. Milyen magasra jut fel a test 
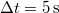alatt? Mekkora a hatásfok? A lejtő és a test közötti súrlódási együttható 
.
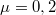Megoldás
- Egyenletes mozgás esetén a lejtőre merőleges és a lejtővel párhuzamos erők is kiegyenlítik egymást. A lejtőre merőleges erők ahol
![\[N=mg\cos\alpha\,,\]](/images/math/5/d/2/5d22eb4f170dfbd2a1e94eb9b9e8a80b.png)
a nyomóerő. A lejtővel párhuzamos erők ahol![\[F=mg\sin\alpha+\mu N\,,\]](/images/math/a/c/e/acefcf5c52ebe1b22da16509f549553e.png)
az általunk kifejtett erő. Egyenletes mozgásnál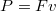 
, így a test sebessége A test tehát![\[v=\frac{P}{F}=\frac{P}{mg(\sin\alpha+\mu\cos\alpha)}\,.\]](/images/math/9/3/b/93b67e7f3e0c25146a6a7787603770f2.png)
idő alatt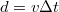 
utat tesz meg, amely alapján a test emelkedése A hasznos energia nyeresége a testnek a nyert helyzeti energiája![\[h=d\sin\alpha= \frac{P \Delta t}{mg(1+\mu\,\mbox{ctg}\,\alpha)}=11,14\,\mathrm{m}\,.\]](/images/math/2/d/e/2de663b9a7a126beacb7c9cc0475d659.png)
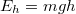, míg a teljes általunk végzett munka 
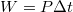. A hatásfok tehát ![\[\eta=\frac{E_{h}}{W}=\frac{1}{1+\mu\,\mbox{ctg}\,\alpha}=0,74\,.\]](/images/math/3/7/5/3753cdfce172a31b34fc583e09a21499.png)
- Egyenletes mozgás esetén a lejtőre merőleges és a lejtővel párhuzamos erők is kiegyenlítik egymást. A lejtőre merőleges erők
