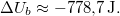„Termodinamika példák - Variációk entrópiaváltozásra” változatai közötti eltérés
A Fizipedia wikiből
(Jelölésbeli konvenciók.) |
|||
| (egy szerkesztő 4 közbeeső változata nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Két test azonos $C=100\,\mathrm{\frac{J}{K}}$ hőkapacitású, de hőmérsékletük különböző: $T_1= | + | </noinclude><wlatex># Két test azonos $C=100\,\mathrm{\frac{J}{K}}$ hőkapacitású, de hőmérsékletük különböző: $T_1=273\,\mathrm{K}$, $T_2=373\,\mathrm{K}$.</wlatex> |
#* a) <wlatex>Mennyi lesz a közös hőmérsékletük, ha termikus kapcsolatba hozzuk őket úgy, hogy a környezet felé ne legyen hőátadás?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$T_k=\frac{T_1+T_2}{2}$$}}</wlatex></includeonly> | #* a) <wlatex>Mennyi lesz a közös hőmérsékletük, ha termikus kapcsolatba hozzuk őket úgy, hogy a környezet felé ne legyen hőátadás?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$T_k=\frac{T_1+T_2}{2}$$}}</wlatex></includeonly> | ||
| − | #* b) <wlatex>Mennyi lesz a közös hőmérséklet, ha a kiegyenlítődést egy reverzíbilisen működő hőerőgép végzi?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$T_k=\sqrt{ | + | #* b) <wlatex>Mennyi lesz a közös hőmérséklet, ha a kiegyenlítődést egy reverzíbilisen működő hőerőgép végzi?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$T_k=\sqrt{T_1 T_2}$$}}</wlatex></includeonly> |
| − | #* c) <wlatex>Ha a kiegyenlítődés nem jár térfogatváltozással, mekkora lesz a két esetben a belső energia megváltozása és az entrópia-változás?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\Delta U_a=0, \qquad \Delta U_b=2C\sqrt{ | + | #* c) <wlatex>Ha a kiegyenlítődés nem jár térfogatváltozással, mekkora lesz a két esetben a belső energia megváltozása és az entrópia-változás?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\Delta U_a=0, \qquad \Delta U_b=2C\sqrt{T_1 T_2}-CT_1-CT_2=-778{,}7\,\mathrm{J},$$ $$\Delta S_a=2C\ln\frac{T_1+T_2}{2}-C\ln T_1-C\ln T_2=2{,}42\,\mathrm{\frac{J}{K}}, \qquad \Delta S_b=0.$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>'''a)''' A két különböző hőmérsékletű test közvetlen kapcsolatba hozása irreverzíbilis folyamat: a rendszerből nem nyerünk ki munkát, a kezdeti állapot pedig csak külső energiabevitellel érhető el újra ( | + | <wlatex>'''a)''' A két különböző hőmérsékletű test közvetlen kapcsolatba hozása irreverzíbilis folyamat: a rendszerből nem nyerünk ki munkát, a kezdeti állapot pedig csak külső energiabevitellel érhető el újra (ld. a ''c)'' pontot is). Nincs térfogatváltozás, egyik test sem végez munkát ($\delta W_1 = \delta W_2 = 0$). A közös $T_{ka}$ hőmérsékletet abból kapjuk meg, hogy az elszigetelt rendszerben az egyik test által leadott hő megegyezik a másik által felvett hővel: |
| − | $$ C( | + | $$ C(T_{ka}-T_1) = C(T_2-T_{ka}), $$ |
innen | innen | ||
| − | $$ | + | $$ T_{ka} = \frac{C T_1 + C T_2}{2C} = \frac{T_1+T_2}{2}. $$ |
| − | '''b)''' A Carnot-körfolyamat reverzíbilis: az ideális hőerőgép által termelt munkát a fordított irányban üzemeltetett gépbe visszatáplálva a kezdeti állapot újra elérhető. Reverzíbilis folyamatokra $\Delta S=0$ | + | '''b)''' A Carnot-körfolyamat reverzíbilis: az ideális hőerőgép által termelt munkát a fordított irányban üzemeltetett gépbe visszatáplálva a kezdeti állapot újra elérhető. Reverzíbilis folyamatokra $\Delta S=0$. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Az entrópiaváltozás általános definíciója | Az entrópiaváltozás általános definíciója | ||
$$ \mathrm{d}S = \frac{\delta Q}{T}, $$ | $$ \mathrm{d}S = \frac{\delta Q}{T}, $$ | ||
| − | amibe helyettesítsük be a közölt hő első főtételből kifejezett | + | amibe helyettesítsük be a közölt hő első főtételből kifejezett $ \delta Q = \mathrm{d}U+p\,\mathrm{d}V $ alakját, ahol $ \mathrm{d}U = C_V\,\mathrm{d}T $: |
| − | + | $$ \mathrm{d}S = C_V \frac{\mathrm{d}T}{T} + \frac{p\,\mathrm{d}V}{T}. $$ | |
| − | alakját, ahol $ \mathrm{d}U= C_V\,\mathrm{d}T $: | + | |
| − | $$ \mathrm{d}S= C_V \frac{\mathrm{d}T}{T} + \frac{p\,\mathrm{d}V}{T}. $$ | + | |
| − | + | Nincs térfogatváltozás, munkavégzés nem történik ($\delta W=p\,\mathrm{d}V=0$, azaz $\delta W_1 = \delta W_2 =0$), a $C$ hőkapacitás az állandó térfogaton mért $C_V$ hőkapacitás. | |
Kiintegrálva a fenti egyenletet a kezdeti- és a végállapot között: | Kiintegrálva a fenti egyenletet a kezdeti- és a végállapot között: | ||
$$ \Delta S_i = C_V \ln\frac{T_{i\text{vég}}}{T_{i\text{kezd}}}. $$ | $$ \Delta S_i = C_V \ln\frac{T_{i\text{vég}}}{T_{i\text{kezd}}}. $$ | ||
A teljes rendszerre | A teljes rendszerre | ||
| − | $$ \Delta S = C \ln\frac{T_k}{T_1} + C \ln\frac{T_k}{T_2} | + | $$ \Delta S = \Delta S_1 + \Delta S_2 |
| − | = 2C \ln\frac{ | + | = C\ln\frac{T_k}{T_1} + C\ln\frac{T_k}{T_2}=C\ln \frac{T_k^2}{T_1 T_2}, $$ |
| + | innen $\Delta S_b=0$ feltétellel | ||
| + | $$ T_{kb} = \sqrt{T_1 T_2}. $$ | ||
| + | |||
| + | '''c)''' '''Az ''a)'' pontban leírt irreverzíbilis esetben''' a teljes rendszert elszigeteltük, összes belső energiája megmarad | ||
| + | $$ \Delta U_a = \Delta U_{1a} + \Delta U_{2a} = 0$$ | ||
| + | és | ||
| + | $$ \Delta U_{1a} = -\Delta U_{2a}. $$ | ||
| + | |||
| + | Mivel nincs térfogatváltozás, a teljes rendszer entrópiaváltozása | ||
| + | $$ \Delta S_a = \Delta S_{1a} + \Delta S_{2a} | ||
| + | = 2C \ln\frac{T_{ka}}{\sqrt{T_1 T_2}} | ||
= 2C \ln \frac{\frac{T_1+ T_2} 2}{\sqrt{T_1 T_2}} \geq 0, $$ | = 2C \ln \frac{\frac{T_1+ T_2} 2}{\sqrt{T_1 T_2}} \geq 0, $$ | ||
| − | most $\Delta | + | most $\Delta S_a \approx 2{,}42\,\mathrm{\frac{J}{K}}$. |
| − | '''A ''b)'' pontban leírt reverzibilis esetben''' nincs | + | '''A ''b)'' pontban leírt reverzibilis esetben''' definíció szerint nincs entrópiaváltozás. |
| − | $$ \Delta | + | $$ \Delta S_b = \Delta S_{1b} + \Delta S_{2b} = 0$$ |
| + | és | ||
| + | $$ \Delta S_{1b} = -\Delta S_{2b}. $$ | ||
| − | + | Nincs térfogatváltozás, munkavégzés nem történik ($\delta W=p\,\mathrm{d}V=0$, azaz $\delta W_1 = \delta W_2 =0$), a $C$ hőkapacitás az állandó térfogaton mért $C_V$ hőkapacitás. | |
| − | $$ \Delta | + | $$ \Delta U_b = \Delta U_{1b} + \Delta U_{2b} |
| − | = C ( | + | = C (T_{kb}-T_1) + C (T_{kb}-T_1) |
| − | = 2C \left( | + | = 2C \left(T_{kb}-\frac{T_1+ T_2} 2\right)=2C\left(\sqrt{T_1 T_2}-\frac{T_1+T_2} 2\right) \leq 0,$$ |
| − | most $\Delta | + | most $\Delta U_b \approx -778{,}7\,\mathrm{J}.$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. május 20., 12:49-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Entrópia, II. főtétel |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Két test azonos
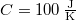hőkapacitású, de hőmérsékletük különböző: 
, 
.
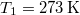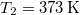- a) Mennyi lesz a közös hőmérsékletük, ha termikus kapcsolatba hozzuk őket úgy, hogy a környezet felé ne legyen hőátadás?
- b) Mennyi lesz a közös hőmérséklet, ha a kiegyenlítődést egy reverzíbilisen működő hőerőgép végzi?
- c) Ha a kiegyenlítődés nem jár térfogatváltozással, mekkora lesz a két esetben a belső energia megváltozása és az entrópia-változás?
Megoldás
a) A két különböző hőmérsékletű test közvetlen kapcsolatba hozása irreverzíbilis folyamat: a rendszerből nem nyerünk ki munkát, a kezdeti állapot pedig csak külső energiabevitellel érhető el újra (ld. a c) pontot is). Nincs térfogatváltozás, egyik test sem végez munkát (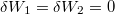
). A közös 
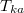hőmérsékletet abból kapjuk meg, hogy az elszigetelt rendszerben az egyik test által leadott hő megegyezik a másik által felvett hővel:
![\[ C(T_{ka}-T_1) = C(T_2-T_{ka}), \]](/images/math/c/4/8/c48e35657b6dd3c4b425d8dc20051561.png)
innen
![\[ T_{ka} = \frac{C T_1 + C T_2}{2C} = \frac{T_1+T_2}{2}. \]](/images/math/b/0/4/b04577e5e9eee48410c4d80a0577cd16.png)
b) A Carnot-körfolyamat reverzíbilis: az ideális hőerőgép által termelt munkát a fordított irányban üzemeltetett gépbe visszatáplálva a kezdeti állapot újra elérhető. Reverzíbilis folyamatokra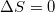 
.
Az entrópiaváltozás általános definíciója
![\[ \mathrm{d}S = \frac{\delta Q}{T}, \]](/images/math/c/b/d/cbd5cf7c09169ef24d1244b4e66f68f5.png)
amibe helyettesítsük be a közölt hő első főtételből kifejezett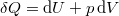 
alakját, ahol 
:
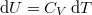![\[ \mathrm{d}S = C_V \frac{\mathrm{d}T}{T} + \frac{p\,\mathrm{d}V}{T}. \]](/images/math/b/7/d/b7d9c413ca9fc690d21a53982e40cdd4.png)
Nincs térfogatváltozás, munkavégzés nem történik (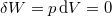
, azaz 
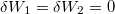), a 
hőkapacitás az állandó térfogaton mért 
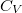hőkapacitás.
Kiintegrálva a fenti egyenletet a kezdeti- és a végállapot között:
![\[ \Delta S_i = C_V \ln\frac{T_{i\text{vég}}}{T_{i\text{kezd}}}. \]](/images/math/4/b/9/4b9aa1cc9ec68247e6eed19721064234.png)
A teljes rendszerre
![\[ \Delta S = \Delta S_1 + \Delta S_2 = C\ln\frac{T_k}{T_1} + C\ln\frac{T_k}{T_2}=C\ln \frac{T_k^2}{T_1 T_2}, \]](/images/math/8/e/c/8ec541fc4e7693a9566d60558b7b1488.png)
innen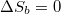 
feltétellel
![\[ T_{kb} = \sqrt{T_1 T_2}. \]](/images/math/5/c/4/5c48f10b52d1b049adfd8a9650d76845.png)
c) Az a) pontban leírt irreverzíbilis esetben a teljes rendszert elszigeteltük, összes belső energiája megmarad
![\[ \Delta U_a = \Delta U_{1a} + \Delta U_{2a} = 0\]](/images/math/e/2/4/e24b1289824970cf3644c6e9b3069343.png)
és
![\[ \Delta U_{1a} = -\Delta U_{2a}. \]](/images/math/d/b/9/db983dcf4aee58fca5a5a81a94213cc5.png)
Mivel nincs térfogatváltozás, a teljes rendszer entrópiaváltozása
![\[ \Delta S_a = \Delta S_{1a} + \Delta S_{2a} = 2C \ln\frac{T_{ka}}{\sqrt{T_1 T_2}} = 2C \ln \frac{\frac{T_1+ T_2} 2}{\sqrt{T_1 T_2}} \geq 0, \]](/images/math/8/4/1/8411b5c8672fe20281c7c76a73336e85.png)
most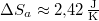 
.
A b) pontban leírt reverzibilis esetben definíció szerint nincs entrópiaváltozás.
![\[ \Delta S_b = \Delta S_{1b} + \Delta S_{2b} = 0\]](/images/math/e/f/0/ef0d8a72013f8a4c42eabba4a97d7201.png)
és
![\[ \Delta S_{1b} = -\Delta S_{2b}. \]](/images/math/3/9/e/39eefe3c5a5a696bc516ec3058a064c0.png)
Nincs térfogatváltozás, munkavégzés nem történik (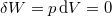, azaz 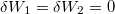), a hőkapacitás az állandó térfogaton mért 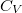hőkapacitás.
![\[ \Delta U_b = \Delta U_{1b} + \Delta U_{2b} = C (T_{kb}-T_1) + C (T_{kb}-T_1) = 2C \left(T_{kb}-\frac{T_1+ T_2} 2\right)=2C\left(\sqrt{T_1 T_2}-\frac{T_1+T_2} 2\right) \leq 0,\]](/images/math/f/d/7/fd7e08c5efd8e2a1a993d56e95c1589f.png)
most 
