„Munka, energia - 2.2.12” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Mechanika - Munka, energia {{Kísérleti fizika gyakorl…”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Egy $m=75\,\mathrm{kg}$ tömegű szánkó két szembenálló $\alpha=30$°-os hajlásszögű lejtős pályán mozog. Az egyik lejtőn elindul lefelé, $s=200\,\mathrm{m}$ út megtétele után leért a lejtő aljára, de a kapott energia tovább viszi a másik lejtőn felfelé. Milyen hosszú utat tesz meg felfelé, ha a súrlódási együttható $\mu=0,03$? | + | </noinclude><wlatex># (2.2.12) Egy $m=75\,\mathrm{kg}$ tömegű szánkó két szembenálló $\alpha=30$°-os hajlásszögű lejtős pályán mozog. Az egyik lejtőn elindul lefelé, $s=200\,\mathrm{m}$ út megtétele után leért a lejtő aljára, de a kapott energia tovább viszi a másik lejtőn felfelé. Milyen hosszú utat tesz meg felfelé, ha a súrlódási együttható $\mu=0,03$? |
</wlatex><includeonly><wlatex>{{Végeredmény|content=$s'=180,2\,\mathrm{m}$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Végeredmény|content=$s'=180,2\,\mathrm{m}$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: Ha felfelé még $s'$ utat tesz meg, akkor a potenciális energia veszteség $$E_{h}-E_{h}'=mgh-mgh'=mg(s-s')\sin\alpha\,.$$ Az energia veszteség megegyezik a súrlódási erő | + | <wlatex>#: Ha felfelé még $s'$ utat tesz meg, akkor a potenciális energia veszteség $$E_{h}-E_{h}'=mgh-mgh'=mg(s-s')\sin\alpha\,.$$ Az energia veszteség megegyezik a súrlódási erő munkájának nagyságával, amely $$W_{s}=-s \mu mg \cos \alpha- s' \mu mg \cos \alpha\,.$$ Így $$s'=s\frac{\mbox{tg}\,\alpha-\mu}{\mbox{tg}\,\alpha+\mu}=180,2\,\mathrm{m}\,.$$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. augusztus 27., 18:55-kori változata
Feladat
- (2.2.12) Egy
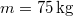tömegű szánkó két szembenálló 
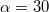°-os hajlásszögű lejtős pályán mozog. Az egyik lejtőn elindul lefelé, 
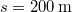út megtétele után leért a lejtő aljára, de a kapott energia tovább viszi a másik lejtőn felfelé. Milyen hosszú utat tesz meg felfelé, ha a súrlódási együttható 
?
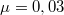Megoldás
- Ha felfelé még
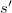utat tesz meg, akkor a potenciális energia veszteség Az energia veszteség megegyezik a súrlódási erő munkájának nagyságával, amely![\[E_{h}-E_{h}'=mgh-mgh'=mg(s-s')\sin\alpha\,.\]](/images/math/5/2/e/52e6157aba074c697fbe68368ea6b04f.png)
Így![\[W_{s}=-s \mu mg \cos \alpha- s' \mu mg \cos \alpha\,.\]](/images/math/5/6/3/5635b8f9238d84ced9fcbb5f8fda064e.png)
![\[s'=s\frac{\mbox{tg}\,\alpha-\mu}{\mbox{tg}\,\alpha+\mu}=180,2\,\mathrm{m}\,.\]](/images/math/7/4/5/7451223bde7aeb93cbc4355bd6ee44be.png)
- Ha felfelé még
