„Munka, energia - Munka számítás 2” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Mechanika - Munka, energia {{Kísérleti fizika gyak…”) |
|||
| 12. sor: | 12. sor: | ||
#: b.) Adjuk meg a gravitációs erő teljes munkáját, amíg a test eljut az $x = 0$ pontba! | #: b.) Adjuk meg a gravitációs erő teljes munkáját, amíg a test eljut az $x = 0$ pontba! | ||
#: c.) Munkatétel alapján adjuk meg a test sebességét az $x = 0$ pontban! | #: c.) Munkatétel alapján adjuk meg a test sebességét az $x = 0$ pontban! | ||
| − | </wlatex><includeonly><wlatex>{{Végeredmény|content= | + | </wlatex><includeonly><wlatex>{{Végeredmény|content=a.) $$dW = - 2 A m g x \, dx$$ b.) $$W = m g A x_0^2$$ c.) $$|v_v| = \sqrt{2 g A x_0^2}$$ }}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: | + | <wlatex>#: a.) A gravitációs erő komponensei $G_x = 0$ és $G_y = - mg$. Tegyük fel, hogy az $x$ helyen vagyunk. Ha elmozdulunk $dx$-el vízszintesen, úgy függőlegesen is el kell mozdulnunk, hogy a pályán maradjunk. A függőleges elmozdulás: $dy = \frac{dy}{dx} dx = 2 A x \,dx$. Az elemi munka így $$dW = \vec{G} d \vec{r} = G_x dx + G_y dy = - m g dy = - 2 A m g x \, dx \; .$$ |
| + | #: b.) $$W = \int dW = \int_{x_0}^0 - 2 A m g x \, dx = \left[ - A m g x^2 \right]_{x_0}^0 = m g A x_0^2 \, .$$ Vegyük észre, hogy amit kaptunk, abban megjelent az $y_0 = A x_0^2$, azaz $W = m g y_0$. Ezt megkaphattuk volna úgy is, ha használjuk azt a tényt, hogy a homogén gravitációs térerőben bevezethető az $E_h = m g h$ helyzeti energia. | ||
| + | #: c.) Munkatétel alapján $$\frac{1}{2} m v_{v}^2 = W \, ,$$ ebből $$v_{v}^2 = 2 g A x_0^2 \, ,$$ azaz $|v_v| = \sqrt{2 g A x_0^2}$. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. október 14., 17:37-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Munka, energia |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy
tömegű kicsiny test egy függőleges szimmetriatengelyű parabola alakú pályán mozoghat, melynek pályaegyenlete 
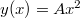. A testre hat a nehézségi erő, a pálya súrlódásmentes. A test nulla kezdősebességgel indul a pálya 
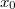koordinátájú pontjából.
- a.) Adjuk meg a gravitációs erő elemi
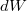munkáját, amikor a test az 
koordinátájú pontból az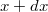 
koordinátájú pontba jut.
- b.) Adjuk meg a gravitációs erő teljes munkáját, amíg a test eljut az
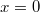pontba!
- c.) Munkatétel alapján adjuk meg a test sebességét az 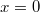pontban!
- a.) Adjuk meg a gravitációs erő elemi
Megoldás
- a.) A gravitációs erő komponensei
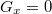és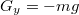 
. Tegyük fel, hogy az helyen vagyunk. Ha elmozdulunk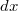 
-el vízszintesen, úgy függőlegesen is el kell mozdulnunk, hogy a pályán maradjunk. A függőleges elmozdulás: 
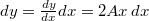. Az elemi munka így ![\[dW = \vec{G} d \vec{r} = G_x dx + G_y dy = - m g dy = - 2 A m g x \, dx \; .\]](/images/math/1/7/1/1711d9e08e1906d9cfb28ea7a6c1c976.png)
- b.) Vegyük észre, hogy amit kaptunk, abban megjelent az
![\[W = \int dW = \int_{x_0}^0 - 2 A m g x \, dx = \left[ - A m g x^2 \right]_{x_0}^0 = m g A x_0^2 \, .\]](/images/math/1/1/d/11d461327aa1f30d0c0d2bcf41f489f9.png)
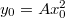, azaz 
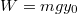. Ezt megkaphattuk volna úgy is, ha használjuk azt a tényt, hogy a homogén gravitációs térerőben bevezethető az 
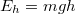helyzeti energia.
- c.) Munkatétel alapján ebből
![\[\frac{1}{2} m v_{v}^2 = W \, ,\]](/images/math/b/0/9/b0941ff32ce5b4d8a0bb7967bfd89d8f.png)
azaz![\[v_{v}^2 = 2 g A x_0^2 \, ,\]](/images/math/e/a/c/eac5d45121110014586f13d3f324dc05.png)
.
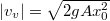- a.) A gravitációs erő komponensei
