„Magnetosztatika példák - Toroid energiája” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
(→Megoldás) |
||
| 15. sor: | 15. sor: | ||
$$L = \frac{N\Phi}{I}$$ | $$L = \frac{N\Phi}{I}$$ | ||
Ebből a tekercs energiája: | Ebből a tekercs energiája: | ||
| − | $$E = \frac{1}{2}LI | + | $$E = \frac{1}{2}LI^2 = \frac{1}{2}N\Phi I$$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2018. április 27., 13:53-kori változata
Feladat
- Egy
menetes toroid vasmagjában 
áramerősség hatására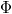 
fluxus jön létre. Mekkora a mágneses tér energiája?
Megoldás
A tekercs öninduktivitása:
![\[L = \frac{N\Phi}{I}\]](/images/math/7/d/7/7d723b721d9dffd9664b01daf0a2ae0d.png)
Ebből a tekercs energiája:
![\[E = \frac{1}{2}LI^2 = \frac{1}{2}N\Phi I\]](/images/math/8/9/8/898980e6b36798506ba9e1925b240464.png)
