„Munka, energia - 2.2.13” változatai közötti eltérés
A Fizipedia wikiből
| 9. sor: | 9. sor: | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># Egy $h$ magasságú $l$ hosszúságú lejtőt egy fém és egy falécből állítunk össze. A pálya felső részéről rövid fémhasábot eresztünk el. A fém és a fa rész hosszának milyen arányánál érjük el, hogy a hasáb a pálya végén megálljon? Mennyi időre van szükség a teljes út megtételére, ha a fémhasáb és a fém súrlódási együtthatója $\mu=0,2$, a fémhasábé és a fáé $\mu'=0,6$, $h=5\,\mathrm{m}$, $l=13\,\mathrm{m}$? | </noinclude><wlatex># Egy $h$ magasságú $l$ hosszúságú lejtőt egy fém és egy falécből állítunk össze. A pálya felső részéről rövid fémhasábot eresztünk el. A fém és a fa rész hosszának milyen arányánál érjük el, hogy a hasáb a pálya végén megálljon? Mennyi időre van szükség a teljes út megtételére, ha a fémhasáb és a fém súrlódási együtthatója $\mu=0,2$, a fémhasábé és a fáé $\mu'=0,6$, $h=5\,\mathrm{m}$, $l=13\,\mathrm{m}$? | ||
| − | </wlatex><includeonly><wlatex>{{Végeredmény|content=$l_{\fém}/l_{fa}=10,71 $ <br> $T=7,26\,\mathrm{s} | + | </wlatex><includeonly><wlatex>{{Végeredmény|content=$l_{\fém}/l_{fa}=10,71$ <br> $T=7,26\,\mathrm{s}$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex>#: A mozgás során a kezdeti mozgási energia teljes mértékben disszipálódik. Ha a lejtő felső, fémből készült szakaszának hosszát $d$-vel jelöljük, akkor az energia mérleg $$mgh=mg\cos\alpha\mu d+ mg\cos\alpha\mu'(l-d)$$ szerint írható fel. A lejtő hajlás szögét a $h=l\sin\alpha$ összefüggésből határozhatjuk meg. Az energia mérlegből kifejezve $$d=\frac{1}{\mu-\mu'}\left(\frac{h}{\cos\alpha}-\mu'l\right)\,,$$ így a fémből és fából készült lejtő darabok hosszúságának aránya $$\frac{d}{l-d}=\frac{h-\mu' l\cos\alpha}{\mu l\cos\alpha-h}=\frac{h-\mu' l\sqrt{1-\left(\frac{h}{l}\right)^{2}}}{\mu l \sqrt{1-\left(\frac{h}{l}\right)^{2}}-h}=\frac{1-\mu' \sqrt{\left(\frac{l}{h}\right)^{2}-1}}{\mu \sqrt{\left(\frac{l}{h}\right)^{2}-1}-1}=10,71$$ <br> A felső szakaszon a gyorsulás nagysága és a mozgás időtartama $$a=g(\sin\alpha-\mu\cos\alpha)\qquad\qquad t=\sqrt{\frac{2d}{a}}\,.$$ Az alsó szakaszon hasonlóan $$a'=g(\mu'\cos\alpha-\sin\alpha)\qquad\qquad t'=\sqrt{\frac{2d}{a'}}\,.$$ A mozgás teljes időtartama $$T=t+t'=\sqrt{\frac{2l(\mu'-\mu)\cos\alpha}{g\left(\frac{h}{l}-\mu\cos\alpha \right)\left(\mu'\cos\alpha-\frac{h}{l}\right)}}=7,26\,\mathrm{s}$$ | <wlatex>#: A mozgás során a kezdeti mozgási energia teljes mértékben disszipálódik. Ha a lejtő felső, fémből készült szakaszának hosszát $d$-vel jelöljük, akkor az energia mérleg $$mgh=mg\cos\alpha\mu d+ mg\cos\alpha\mu'(l-d)$$ szerint írható fel. A lejtő hajlás szögét a $h=l\sin\alpha$ összefüggésből határozhatjuk meg. Az energia mérlegből kifejezve $$d=\frac{1}{\mu-\mu'}\left(\frac{h}{\cos\alpha}-\mu'l\right)\,,$$ így a fémből és fából készült lejtő darabok hosszúságának aránya $$\frac{d}{l-d}=\frac{h-\mu' l\cos\alpha}{\mu l\cos\alpha-h}=\frac{h-\mu' l\sqrt{1-\left(\frac{h}{l}\right)^{2}}}{\mu l \sqrt{1-\left(\frac{h}{l}\right)^{2}}-h}=\frac{1-\mu' \sqrt{\left(\frac{l}{h}\right)^{2}-1}}{\mu \sqrt{\left(\frac{l}{h}\right)^{2}-1}-1}=10,71$$ <br> A felső szakaszon a gyorsulás nagysága és a mozgás időtartama $$a=g(\sin\alpha-\mu\cos\alpha)\qquad\qquad t=\sqrt{\frac{2d}{a}}\,.$$ Az alsó szakaszon hasonlóan $$a'=g(\mu'\cos\alpha-\sin\alpha)\qquad\qquad t'=\sqrt{\frac{2d}{a'}}\,.$$ A mozgás teljes időtartama $$T=t+t'=\sqrt{\frac{2l(\mu'-\mu)\cos\alpha}{g\left(\frac{h}{l}-\mu\cos\alpha \right)\left(\mu'\cos\alpha-\frac{h}{l}\right)}}=7,26\,\mathrm{s}$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 13., 10:56-kori változata
Feladat
- Egy
 magasságú
magasságú  hosszúságú lejtőt egy fém és egy falécből állítunk össze. A pálya felső részéről rövid fémhasábot eresztünk el. A fém és a fa rész hosszának milyen arányánál érjük el, hogy a hasáb a pálya végén megálljon? Mennyi időre van szükség a teljes út megtételére, ha a fémhasáb és a fém súrlódási együtthatója
hosszúságú lejtőt egy fém és egy falécből állítunk össze. A pálya felső részéről rövid fémhasábot eresztünk el. A fém és a fa rész hosszának milyen arányánál érjük el, hogy a hasáb a pálya végén megálljon? Mennyi időre van szükség a teljes út megtételére, ha a fémhasáb és a fém súrlódási együtthatója 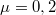 , a fémhasábé és a fáé
, a fémhasábé és a fáé 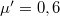 ,
, 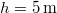 ,
, 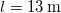 ?
?
Megoldás
- A mozgás során a kezdeti mozgási energia teljes mértékben disszipálódik. Ha a lejtő felső, fémből készült szakaszának hosszát
 -vel jelöljük, akkor az energia mérleg szerint írható fel. A lejtő hajlás szögét a
-vel jelöljük, akkor az energia mérleg szerint írható fel. A lejtő hajlás szögét a![\[mgh=mg\cos\alpha\mu d+ mg\cos\alpha\mu'(l-d)\]](/images/math/1/8/8/188401c9e5844245145e57aab3d2bb92.png)
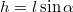 összefüggésből határozhatjuk meg. Az energia mérlegből kifejezve így a fémből és fából készült lejtő darabok hosszúságának aránya
összefüggésből határozhatjuk meg. Az energia mérlegből kifejezve így a fémből és fából készült lejtő darabok hosszúságának aránya![\[d=\frac{1}{\mu-\mu'}\left(\frac{h}{\cos\alpha}-\mu'l\right)\,,\]](/images/math/b/0/d/b0db7067d7bcb5810629949dfdc15b06.png)
![\[\frac{d}{l-d}=\frac{h-\mu' l\cos\alpha}{\mu l\cos\alpha-h}=\frac{h-\mu' l\sqrt{1-\left(\frac{h}{l}\right)^{2}}}{\mu l \sqrt{1-\left(\frac{h}{l}\right)^{2}}-h}=\frac{1-\mu' \sqrt{\left(\frac{l}{h}\right)^{2}-1}}{\mu \sqrt{\left(\frac{l}{h}\right)^{2}-1}-1}=10,71\]](/images/math/8/0/2/802f595f614a8165cdbf0e34f84fb73a.png)
A felső szakaszon a gyorsulás nagysága és a mozgás időtartamaAz alsó szakaszon hasonlóan![\[a=g(\sin\alpha-\mu\cos\alpha)\qquad\qquad t=\sqrt{\frac{2d}{a}}\,.\]](/images/math/1/d/6/1d6bba3214f7a8d2cbe4f40d7656eff2.png) A mozgás teljes időtartama
A mozgás teljes időtartama![\[a'=g(\mu'\cos\alpha-\sin\alpha)\qquad\qquad t'=\sqrt{\frac{2d}{a'}}\,.\]](/images/math/9/7/3/973efecdc4aafa6dc3ef253dfbcaca84.png)
![\[T=t+t'=\sqrt{\frac{2l(\mu'-\mu)\cos\alpha}{g\left(\frac{h}{l}-\mu\cos\alpha \right)\left(\mu'\cos\alpha-\frac{h}{l}\right)}}=7,26\,\mathrm{s}\]](/images/math/5/8/5/585ad03fc23e464fd31d6489ff940472.png)
- A mozgás során a kezdeti mozgási energia teljes mértékben disszipálódik. Ha a lejtő felső, fémből készült szakaszának hosszát