„Termodinamika példák - Entrópiaváltozás egyensúlyig kaloriméterben” változatai közötti eltérés
A Fizipedia wikiből
| 18. sor: | 18. sor: | ||
Az entrópiaváltozás a részrendszerek entrópiaváltozásának összege: | Az entrópiaváltozás a részrendszerek entrópiaváltozásának összege: | ||
| − | $$ \Delta S = \int_{T_1}^{T_k} \frac{c_1 m_1} T\,\mathrm{d}T+ \int_{T_2}^{T_k} \frac{c_2 m_2} T\,\mathrm{d}T | + | $$ \Delta S = \int_{T_1}^{T_k} \frac{c_1 m_1} T\,\mathrm{d}T + \int_{T_2}^{T_k} \frac{c_2 m_2} T\,\mathrm{d}T |
= c_1 m_1 \ln\frac{T_k}{T_1} + c_2 m_2 \ln\frac{T_k}{T_2} | = c_1 m_1 \ln\frac{T_k}{T_1} + c_2 m_2 \ln\frac{T_k}{T_2} | ||
\approx - 23,\!57 \mathrm{\frac{J}{K}} + 27,\!03 \mathrm{\frac{J}{K}} | \approx - 23,\!57 \mathrm{\frac{J}{K}} + 27,\!03 \mathrm{\frac{J}{K}} | ||
| − | = 3,\!46 \mathrm{\frac{J}{K}. $$ | + | = 3,\!46 \mathrm{\frac{J}{K}}. $$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 15., 22:39-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Entrópia, II. főtétel |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
-
, 
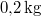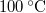hőmérsékletű vasat hőszigetelt kaloriméterben lévő, 
, 
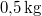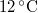-os vízbe teszünk. A vas fajhője 
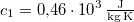, a vízé 
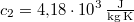. Mennyi az entrópia-változás a hőmérséklet kiegyenlítődése miatt, ha a nyomás állandó?
Megoldás
A közös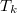 
hőmérsékletet úgy kapjuk meg, ha felírjuk, hogy a vas által leadott hő megegyezik a víz által felvett hővel:
![\[ c_1 m_1\left(T_1-T_k\right)= c_2 m_2\left(T_k-T_2\right), \]](/images/math/7/5/d/75df2116d676d59faaa8d2eb0914be77.png)
ahol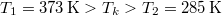 
a vas kezdeti, a közös és víz kezdeti hőmérséklete, 
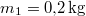a vas, 
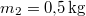a víz hőmérséklete.
![\[ T_k = \frac{c_1 m_1 T_1+ c_2 m_2 T_2}{c_1 m_1+ c_2 m_2}\approx 288,\!71\,\mathrm{K}. \]](/images/math/7/b/3/7b30daae58d622b008bab37935fc00f1.png)
Az entrópiaváltozás a részrendszerek entrópiaváltozásának összege:
![\[ \Delta S = \int_{T_1}^{T_k} \frac{c_1 m_1} T\,\mathrm{d}T + \int_{T_2}^{T_k} \frac{c_2 m_2} T\,\mathrm{d}T = c_1 m_1 \ln\frac{T_k}{T_1} + c_2 m_2 \ln\frac{T_k}{T_2} \approx - 23,\!57 \mathrm{\frac{J}{K}} + 27,\!03 \mathrm{\frac{J}{K}} = 3,\!46 \mathrm{\frac{J}{K}}. \]](/images/math/b/0/5/b0533c522d0e5219ef32d368fe8df685.png)
