„Magnetosztatika példák - Eltolási áram síkkondenzátorban” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 2. Kategória:Szerkesztő:Beleznai Kategória:Magnetosztatika {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex>#Határozzuk meg, mekkora az eltolási áram, olyan síkkondenzátor esetén, amelynek lemezei egymással párhuzamosak maradnak, miközben $u$ sebességgel távolodnak egymástól, ha <br> '''a)''' az $\omega$ töltéssűrűság állandó <br> '''b)''' a lemezek közötti feszültség állandó. <br> </wlatex><includeonly><wlatex>{{Végeredmény|content='''a)'''$$\frac{\partial D}{\partial t} = 0$$ <br> | + | </noinclude><wlatex>#Határozzuk meg, mekkora az eltolási áram, olyan síkkondenzátor esetén, amelynek lemezei egymással párhuzamosak maradnak, miközben $u$ sebességgel távolodnak egymástól, ha <br> '''a)''' az $\omega$ töltéssűrűság állandó <br> '''b)''' a lemezek közötti feszültség állandó. <br> </wlatex><includeonly><wlatex>{{Végeredmény|content='''a)'''$$\frac{\partial D}{\partial t} = 0$$ <br> '''b)''' $$\frac{\partial D}{\partial t} = -\frac{U \epsilon_0}{ut^2}$$}} |
| − | + | ||
| − | '''b)''' $$\frac{\partial D}{\partial t} = -\frac{U \epsilon_0}{ut^2}$$}} | + | |
</wlatex></includeonly><noinclude> | </wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
A lap 2013. július 15., 18:22-kori változata
Feladat
- Határozzuk meg, mekkora az eltolási áram, olyan síkkondenzátor esetén, amelynek lemezei egymással párhuzamosak maradnak, miközben
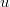sebességgel távolodnak egymástól, ha
a) az
töltéssűrűság állandó
b) a lemezek közötti feszültség állandó.
Megoldás
a, Mivel állandó ezért a dielektromos eltolás vektora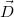 
is állandó a kondenzátor lemezei között, ezért az eltolási áram értéke zérus. Vagyis:
![\[\frac{\partial D}{\partial t} = 0\]](/images/math/1/c/c/1cc2bd06331a5f4b5abd0bb327a36516.png)
b, Ha kondenzátor lemezei között az 
feszültség állandó, akkor:
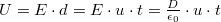Amiből:
![\[D = \frac{\epsilon_0 U}{ut}\]](/images/math/0/9/b/09b52911ae0d981b405d57a99440edf7.png)
Ezzel az etolási áram pedig:
![\[\frac{\partial D}{\partial t} = -\frac{U \epsilon_0}{ut^2}\]](/images/math/0/b/4/0b4c599dac950846ccaeceb05815b655.png)
