„Munka, energia - 2.3.11” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
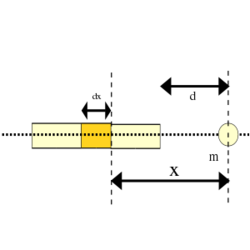
| − | </noinclude><wlatex># Milyen nagyságú gravitációs vonzóerőt fejt ki egy $l$ hosszúságú, kis $q$ keresztmetszetű, $\rho$ sűrűségű homogén rúd a tengelyének irányában, a végpontjától $d$ távolságra levő $m$ tömegű tömegpontra?[[Kép:Kfgy_2_3_11.svg|none|250px]] | + | </noinclude><wlatex># (2.3.11) Milyen nagyságú gravitációs vonzóerőt fejt ki egy $l$ hosszúságú, kis $q$ keresztmetszetű, $\rho$ sűrűségű homogén rúd a tengelyének irányában, a végpontjától $d$ távolságra levő $m$ tömegű tömegpontra?[[Kép:Kfgy_2_3_11.svg|none|250px]] |
</wlatex><includeonly><wlatex>{{Útmutatás|content=Osszuk fel a rudat kis $dx$ hosszúságú szakaszokra, majd ezek hatását összegezzük!}}{{Végeredmény|content=$$F_{g}=\frac{\gamma m\rho q l}{d(d+l)}$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content=Osszuk fel a rudat kis $dx$ hosszúságú szakaszokra, majd ezek hatását összegezzük!}}{{Végeredmény|content=$$F_{g}=\frac{\gamma m\rho q l}{d(d+l)}$$}}</wlatex></includeonly><noinclude> | ||
A lap 2013. augusztus 27., 21:34-kori változata
Feladat
- (2.3.11) Milyen nagyságú gravitációs vonzóerőt fejt ki egy
hosszúságú, kis 
keresztmetszetű, 
sűrűségű homogén rúd a tengelyének irányában, a végpontjától 
távolságra levő 
tömegű tömegpontra?
Megoldás
- Vegyük fel a vonatkoztatási rendszert úgy, hogy az origó a rúdnak a testhez közelebbi végében van rögzítve, az
tengely pedig a rúd irányába mutat. Ekkor a test koordinátája 
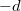. Osszuk fel a rudat kis 
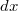hosszúságú darabkákra. Az koordinátánál található kis darabka tömege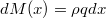 
, és az tömegű testtől való távolsága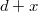 
. Így a kis darabka által az tömegű testre kifejtett gravitációs erő A feladatban az a kérdés, hogy mekkora az egész rúd által kifejtett gravitációs erő. Ehhez összegeznünk kell az összes kis![\[dF_{g}(x)=\gamma\frac{mdM(x)}{(d+x)^{2}}=\frac{\gamma m\rho q}{(d+x)^{2}}dx\,.\]](/images/math/0/8/c/08cfbb72f06f35107e1d5e9ea016eb0b.png)
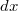hosszúságú darabka járulékát. A 
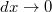határesetben az összegzés helyett integrálni kell. ![\[F_{g}=\int dF_{g}(x)=\int_{0}^{l}\frac{\gamma m\rho q}{(d+x)^{2}}dx=\frac{\gamma m\rho q l}{d(d+l)}\]](/images/math/4/a/0/4a086e25aa50f5f0aa3aada4f780f10e.png)
- Vegyük fel a vonatkoztatási rendszert úgy, hogy az origó a rúdnak a testhez közelebbi végében van rögzítve, az
