„Magnetosztatika példák - Vezetőkeretre ható forgatónyomaték” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
(→Megoldás) |
||
| 34. sor: | 34. sor: | ||
Ahol $\vec{A}$ a keret síkjának normálisa irányába mutat, nagysága a keret területével egyezik. A mi esetünkben $\vec{B}$ és $\vec{A}$ egymással $90^o-45^o=45^o$ szöget szár be, így a forgatónyomaték nagysága a két esetben a következőképp alakul: | Ahol $\vec{A}$ a keret síkjának normálisa irányába mutat, nagysága a keret területével egyezik. A mi esetünkben $\vec{B}$ és $\vec{A}$ egymással $90^o-45^o=45^o$ szöget szár be, így a forgatónyomaték nagysága a két esetben a következőképp alakul: | ||
| − | $$M_1= | + | $$M_1=IA_1B \sin(45^o)=I\dfrac{l^2B \sqrt{2}}{32}$$ |
| − | $$M_2= | + | $$M_2=IA_2B \sin(45^o)=I\dfrac{l^2B \sqrt{2}}{8\pi}$$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. szeptember 30., 13:52-kori változata
Feladat
- Egy
hosszúságú vezető darabból egy négyzet alakú, majd más alkalommal egy kör alakú hurkot készítünk, és mindkét esetben 
indukciójú homogén mágneses térbe helyezzük. A keret síkja mindegyik esetben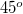 
-os szöget zár be a mágneses erőtérrel, a keretben pedig 
erősségű áram folyik. Határozzuk meg a keretre ható forgatónyomatékot mindkét esetben.
Megoldás
A szögletes keret oldalhossza:
![\[a=\dfrac{l}{4}\]](/images/math/d/b/5/db5a6675028f3df8c9a4cfb58bb32ad5.png)
A kör alakú gyűrű sugara:
![\[r=\dfrac{l}{2\pi}\]](/images/math/6/a/a/6aac73dfdf811ecada2d98145abd0eb0.png)
A szögletes keret területe:
![\[A_1=a^2=\dfrac{l^2}{16}\]](/images/math/9/1/3/9132688571970fd082f77c4a8d977691.png)
A kör alakú keret területe:
![\[A_2=r^2 \pi=\dfrac{l^2}{4\pi}\]](/images/math/4/a/1/4a1ab4635927663693fe812a781f398a.png)
áram által átjárt 
területű keretre ható forgatónyomaték a mágneses dipólmomentum és a mágneses indukció vektor vektorszorzata:
![\[\vec{M}=\vec{P}\times\vec{B} = I\cdot\vec{A}\times\vec{B} \]](/images/math/0/b/1/0b1385814db448ca853f427bc38d9b48.png)
Ahol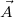 
a keret síkjának normálisa irányába mutat, nagysága a keret területével egyezik. A mi esetünkben 
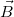és 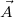egymással 
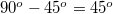szöget szár be, így a forgatónyomaték nagysága a két esetben a következőképp alakul:
![\[M_1=IA_1B \sin(45^o)=I\dfrac{l^2B \sqrt{2}}{32}\]](/images/math/c/a/e/cae0be15ce4fb981cf79f9ce17fb7952.png)
![\[M_2=IA_2B \sin(45^o)=I\dfrac{l^2B \sqrt{2}}{8\pi}\]](/images/math/0/0/1/001b87322df4da81aab4ffb520410570.png)
