„Munka, energia - 2.3.6” változatai közötti eltérés
A Fizipedia wikiből
a (→Feladat) |
(→Feladat) |
||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex>#(*2.3.6) | + | </noinclude><wlatex>#(*2.3.6 alapján) |
| − | </wlatex><includeonly><wlatex>{{Útmutatás|content= | + | #: a.) Első kozmikus sebességnek nevezzük azt a sebességet, amennyivel a Föld felszínén vízszintesen el kell lőni egy testet, hogy körpályán megkerülje a Földet, feltéve hogy nincs légellenállás. Mekkora az első kozmikus sebesség a Földön? |
| + | #: b.) Második kozmikus sebességnek nevezzük azt a sebességet, amennyivel elindítva egy testet a Föld felszínéről, el tud szabadulni a Földtől. Mekkora a második kozmikus sebesség? | ||
| + | #: (Adatok: $R_{F} = 6370 km$, $g_{0} = 9.81 m/s^2$) | ||
| + | </wlatex><includeonly><wlatex>{{Útmutatás|content=Az első feladatban írjuk fel a körpályán való mozgásra a Newton egyenletet. A második feladatban számítsuk ki, mekkora munkát végez a gravitációs erő amíg a test eljut a végtelen messzi pontba. Ezután munkatétel.}}{{Végeredmény|content=$v_1 = 7.9 km/s$ <br> $v_2 = 11.2 km/s$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
A lap 2014. október 14., 10:24-kori változata
Feladat
- (*2.3.6 alapján)
- a.) Első kozmikus sebességnek nevezzük azt a sebességet, amennyivel a Föld felszínén vízszintesen el kell lőni egy testet, hogy körpályán megkerülje a Földet, feltéve hogy nincs légellenállás. Mekkora az első kozmikus sebesség a Földön?
- b.) Második kozmikus sebességnek nevezzük azt a sebességet, amennyivel elindítva egy testet a Föld felszínéről, el tud szabadulni a Földtől. Mekkora a második kozmikus sebesség?
- (Adatok:
, 
)
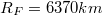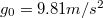Megoldás
- A Föld gravitációs mezejében az
tömegű test potenciális energiája a Föld középpontjától![\[V(r)=-\gamma\frac{Mm}{r}\qquad\gamma=6,67\cdot 10^{-11}\,\mathrm{\frac{Nm^{2}}{kg^{2}}}\]](/images/math/3/2/0/3201ce02c7d00c4b7d1f7523cc6be835.png)
távolságban. A Föld felszínén a test potenciális energiája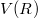 
. Ha a légellenállástól eltekintünk, akkor a szökési sebesség az a 
sebesség, melyre Az ekkora sebességre való felgyorsításhoz szükséges teljesítmény![\[V(R)+\frac{1}{2}mv^{2}=V(r\rightarrow\infty)\qquad\Rightarrow\qquad v=\sqrt{\frac{2\gamma M}{R}}=1,11\cdot 10^{4}\,\mathrm{\frac{m}{s}}\,.\]](/images/math/3/0/e/30e1452cf22c24254c9a93d838291ec5.png)
ha eltekintünk a gyorsítás során megtett úttól.![\[P=\frac{\frac{1}{2}mv^{2}}{\Delta t}=6,16\cdot 10^{7}W\,,\]](/images/math/7/7/b/77bfdafe04312509cc73f4a9da4cfcef.png)
- A Föld gravitációs mezejében az
