„Termodinamika példák - Entrópiaváltozás hőcserében” változatai közötti eltérés

A lap 2013. április 13., 19:19-kori változata (lapforrás) Stippinger (vitalap | szerkesztései) (Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Termodinamika - Entrópia, II. főtétel {{Kísérleti fizi…”)		A lap 2013. április 13., 23:49-kori változata (lapforrás) Stippinger (vitalap | szerkesztései) Újabb szerkesztés →
17. sor:		17. sor:
	== Megoldás ==		== Megoldás ==
−	<wlatex>Megoldás szövege	+	<wlatex>$m=1\,\mathrm{\,\mathrm{kg}}$, $ T_0=273\,\mathrm K$, $ T_H=373\,\mathrm K$
		+
		+	'''a)''' A víz a közölt $\delta Q=cm\mathrm{d}T$ hőt az aktuális $T$ hőmérsékletén veszi fel:
		+	$$ \Delta S_\text{víz}=\int_{T_0}^{T_H} \frac{\delta Q}{T}=cm\ln \frac{T_H}{T_0}. $$
		+
		+	'''b)''' A hőtartály hőmérséklete állandóan $T_H$, az általa leadott összes hőmennyiség nagysága megegyezik a víz által felvettel:
		+	$$ \Delta S_\text{hőtartály} = \frac{\Delta Q}{T_H} = \frac{-cm(T_H-T_0)}{T_H} = cm\left(\frac{T_0}{T_H}-1\right). $$
		+
		+	'''c)''' A teljes rendszer (vagy az univerzum) entrópiaváltozása a folyamat következtében
		+	$$ \Delta S = \Delta S_\text{víz} + \Delta S_\text{hőtartály}
		+	= cm\left(\left(\frac{T_0}{T_H}-1\right)-\ln \frac{T_0}{T_H}\right) \ge 0$$
		+
		+	'''d)''' Ha beiktatunk egy közbülső, $T_i\,\mathrm{K}$ hőmérsékletű hőtartályt, a víz entrópiaváltozása ugyanaz marad:
		+	$$ \Delta S_\text{víz}=\int_{T_0}^{T_i} \frac{\delta Q}{T}+\int_{T_i}^{T_H} \frac{\delta Q}{T}=\int_{T_0}^{T_H} \frac{\delta Q}{T}=cm\ln \frac{T_H}{T_0}, $$
		+	a hőtartályok viszont összességében is kisebb entrópianövekedést szenvednek el:
		+	$$ \Delta S_\text{hőtartályok} = \frac{\Delta Q}{T_H} = \frac{-cm(T_i-T_0)}{T_i} + \frac{-cm(T_H-T_i)}{T_H}
		+	= cm\left(\frac{T_0}{T_i}+\frac{T_i}{T_H}-2\right). $$
		+	A teljes rendszer entrópia
		+	$$ \Delta S = cm \left(\frac{T_0}{T_i}+\frac{T_i}{T_H}-2 - \ln \frac{T_0}{T_H}\right), $$
		+	ami kisebb, mint ''c)''-ben.
		+
		+	==== Megjegyzés ====
		+	Behelyettesítés nélkül a
		+	$$ \Delta S = cm \left(\frac{T_0}{T_H}-1-\left[1+\frac{T_0}{T_H}-\frac{T_0}{T_i}-\frac{T_i}{T_H}\right]\right)$$ átalakítással tetszőleget $T_0<T_i<T_H$ értékre látható, hogy a ''c)''-ben kapottnál kiseb érték adódott.
		+	A $\Delta S_\text{hőtartályok} (T_i) = cm \left(\frac{T_0}{T_i}+\frac{T_i}{T_H}-2\right)$ függvény szélsőértékvizsgálatával belátható, hogy a legkisebb entrópiaváltozáshoz vezető hőmérséklet $T_i=\sqrt{T_0 T_H}$, a hozzá tartozó entrópiaváltozás $\Delta S_\text{hőtartályok,min} = 2cm \left(\sqrt{\frac{T_0}{T_H}}-1\right)$
		+
		+	'''e)''' Láttuk, hogy egy köztes hőtartály csökkenti az entrópia-növekedést. Használjunk $N\to\infty$ darab hőtartályt ekvidisztáns $\Delta T = \frac{T_H-T_0}{N}\to0$ hőmérsékletkülönbségekkel!
		+
		+	A víz entrópiaváltozása most is
		+	$$ \Delta S_\text{víz}=\int_{T_0}^{T_H} \frac{\delta Q}{T}=cm\ln \frac{T_H}{T_0} $$
		+	lesz, mivel a köztes hőmérsékletek kiesnek a képletből
		+
		+	A hőtartályokra:
		+	$$ \Delta S_\text{hőtartályok} = \lim_{\substack{N\to\infty \\ \Delta T\to0}}
		+	cm \left(\frac{\Delta T}{T_1}+\frac{\Delta T}{T_2}+\ldots+\frac{\Delta T}{T_N}\right)=$$
		+	$$ = -cm \lim_{\substack{N\to\infty \\ \Delta T\to0}} \sum _{i=1}^N\frac{\Delta T}{T_i}
		+	= cm\int_{T_0}^{T_H}\frac{\mathrm{d}T}{T}=-cm\ln \frac{T_H}{T_0} $$
		+
		+	Tehát így $\Delta S = \Delta S_\text{víz} + \Delta S_\text{hőtartályok}=0$ tetszőlegesen megközelíthető.
	</wlatex>		</wlatex>
	</noinclude>		</noinclude>

---

A lap 2013. április 13., 23:49-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája: Kinetikus gázelmélet, transzport Állapotváltozás, I. főtétel Fajhő, Körfolyamatok Entrópia, II. főtétel Homogén rendszerek Fázisátalakulások Kvantummechanikai bevezető
Entrópia, II. főtétel
Feladatok listája: Izoterm tágulás Izobár táguláskor S(T,V), adiabata Id. g. entrópiája Forralás Hőcsere Carnot-körfolyamat Keveredési entrópia Gibbs-paradoxon Kaloriméterben Entrópiaváltozások
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

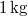1. tömegű, 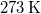hőmérsékletű vizet termikus kapcsolatba hozunk egy 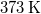hőmérsékletű hőtartállyal.
   • a) Mekkora a víz entrópia-változása, miután a hőmérséklete elérte a hőtartály hőmérsékletét?
   • b) Mekkora eközben a hőtartály entrópia-változása?
   • c) Mekkora a teljes rendszerben (hőtartály és víz) létrejött entrópia-változás?
   • d) Mennyi a teljes rendszerben létrejött entrópia-változás, ha a testet először egy 323 K hőmérsékletű hőtartállyal, majd az egyensúly beállta után a 373 K hőmérsékletű hőtartállyal hozzuk kapcsolatba?
   • e) Lehet-e úgy melegíteni a vizet, hogy a teljes rendszer entrópia-változása kisebb legyen egy előírt értéknél (vagyis a folyamat előírt mértékben megközelítse a reverzíbilis folyamatot)?

Megoldás

, ,

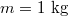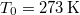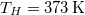
a) A víz a közölt 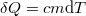hőt az aktuális hőmérsékletén veszi fel:

b) A hőtartály hőmérséklete állandóan 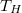, az általa leadott összes hőmennyiség nagysága megegyezik a víz által felvettel:

c) A teljes rendszer (vagy az univerzum) entrópiaváltozása a folyamat következtében

d) Ha beiktatunk egy közbülső, 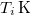hőmérsékletű hőtartályt, a víz entrópiaváltozása ugyanaz marad:

a hőtartályok viszont összességében is kisebb entrópianövekedést szenvednek el:

A teljes rendszer entrópia

ami kisebb, mint c)-ben.

Megjegyzés

Behelyettesítés nélkül a

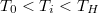átalakítással tetszőleget értékre látható, hogy a c)-ben kapottnál kiseb érték adódott.

A 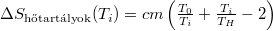függvény szélsőértékvizsgálatával belátható, hogy a legkisebb entrópiaváltozáshoz vezető hőmérséklet 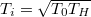, a hozzá tartozó entrópiaváltozás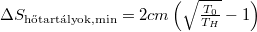

e) Láttuk, hogy egy köztes hőtartály csökkenti az entrópia-növekedést. Használjunk 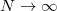darab hőtartályt ekvidisztáns 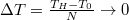hőmérsékletkülönbségekkel!

A víz entrópiaváltozása most is

lesz, mivel a köztes hőmérsékletek kiesnek a képletből

A hőtartályokra:

Tehát így 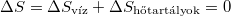tetszőlegesen megközelíthető.