„Termodinamika példák - Variációk entrópiaváltozásra” változatai közötti eltérés
| 47. sor: | 47. sor: | ||
= 2C \ln\frac{T_k}{\sqrt{T_1 T_2}} | = 2C \ln\frac{T_k}{\sqrt{T_1 T_2}} | ||
= 2C \ln \frac{\frac{T_1+ T_2} 2}{\sqrt{T_1 T_2}} \geq 0, $$ | = 2C \ln \frac{\frac{T_1+ T_2} 2}{\sqrt{T_1 T_2}} \geq 0, $$ | ||
| − | most $\Delta S \approx 202, | + | most $\Delta S \approx 202{,}44 \mathrm{\frac{J}{K}}$. |
| 58. sor: | 58. sor: | ||
= C (T_k-T_1) + C (T_k-T_1) | = C (T_k-T_1) + C (T_k-T_1) | ||
= 2C \left(T_k-\frac{T_1+ T_2} 2\right)=2C\left(\sqrt{T_1 T_2}-\frac{T_1+ T_2} 2\right) \leq 0,$$ | = 2C \left(T_k-\frac{T_1+ T_2} 2\right)=2C\left(\sqrt{T_1 T_2}-\frac{T_1+ T_2} 2\right) \leq 0,$$ | ||
| − | most $\Delta U \approx -778, | + | most $\Delta U \approx -778{,}69 \mathrm{J}.$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 16., 11:50-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Entrópia, II. főtétel |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Két test azonos
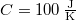hőkapacitású, de hőmérsékletük különböző: 
, 
.
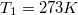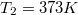- a) Mennyi lesz a közös hőmérsékletük, ha termikus kapcsolatba hozzuk őket úgy, hogy a környezet felé ne legyen hőátadás?
- b) Mennyi lesz a közös hőmérséklet, ha a kiegyenlítődést egy reverzíbilisen működő hőerőgép végzi?
- c) Ha a kiegyenlítődés nem jár térfogatváltozással, mekkora lesz a két esetben a belső energia megváltozása és az entrópia-változás?
Megoldás
a) A két különböző hőmérsékletű test közvetlen kapcsolatba hozása irreverzíbilis folyamat: a rendszerből nem nyerünk ki munkát, a kezdeti állapot pedig csak külső energiabevitellel érhető el újra (lásd a c) pontot is). A közös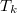 
hőmérsékletet úgy kapjuk meg, ha felírjuk, hogy az elszigetelt rendszerben az egyik test által leadott hő megegyezik a másik által felvett hővel:
![\[ C(T_k-T_1) = C(T_2-T_k), \]](/images/math/a/2/5/a25362f64205c45a5bc7de569e65272a.png)
innen
![\[ T_k=\frac{C T_1+C T_2}{\mathrm{2C}}=\frac{T_1+ T_2} 2.\]](/images/math/a/8/e/a8e6890c80252b988f1bc30ea045a687.png)
b) A Carnot-körfolyamat reverzíbilis: az ideális hőerőgép által termelt munkát a fordított irányban üzemeltetett gépbe visszatáplálva a kezdeti állapot újra elérhető. Reverzíbilis folyamatokra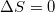 
:
![\[ \Delta S = \Delta S_1 + \Delta S_2 = C\ln\frac{T_k}{T_1} + C\ln\frac{T_k}{T_2}=C\ln \frac{T_k^2}{T_1 T_2}=0, \]](/images/math/9/7/d/97df9bf62c3e0e12550e1391256a5cbf.png)
innen
![\[ T_k=\sqrt{T_1 T_2}.\]](/images/math/4/4/a/44a2d05cbb5791dac4d67346f880238a.png)
c) Az a) pontban leírt irreverzíbilis esetben a teljes rendszert elszigeteltük, összes belső energiája megmarad
![\[ \Delta U = \Delta U_1 + \Delta U_2 = 0\]](/images/math/3/0/2/30200fd173d3b6ac2db2c23770aa7c62.png)
és
![\[ \Delta U_1 = -\Delta U_2. \]](/images/math/3/9/e/39e3e13a8e76b8632fce5d812af08166.png)
Az entrópiaváltozás általános definíciója
![\[ \mathrm{d}S = \frac{\delta Q}{T}, \]](/images/math/c/b/d/cbd5cf7c09169ef24d1244b4e66f68f5.png)
amibe helyettesítsük be a közölt hő első főtételből kifejezett
![\[ \delta Q = \mathrm{d}U+p\,\mathrm{d}V \]](/images/math/f/2/1/f2158c0604f29f1f878df0d5c9709b7f.png)
alakját, ahol 
:
![\[ \mathrm{d}S= C_V \frac{\mathrm{d}T}{T} + \frac{p\,\mathrm{d}V}{T}. \]](/images/math/9/2/d/92d483cebee56f48a4e75a0814ddd76e.png)
Most nincs térfogatváltozás, munkavégzés nem történik (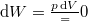
, azaz 
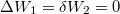), a 
hőkapacitás az állandó térfogaton mért 
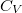hőkapacitás.
Kiintegrálva a fenti egyenletet a kezdeti- és a végállapot között:
![\[ \Delta S_i = C_V \ln\frac{T_{i\text{vég}}}{T_{i\text{kezd}}}. \]](/images/math/4/b/9/4b9aa1cc9ec68247e6eed19721064234.png)
A teljes rendszerre
![\[ \Delta S = C \ln\frac{T_k}{T_1} + C \ln\frac{T_k}{T_2} = 2C \ln\frac{T_k}{\sqrt{T_1 T_2}} = 2C \ln \frac{\frac{T_1+ T_2} 2}{\sqrt{T_1 T_2}} \geq 0, \]](/images/math/7/0/2/702ff94977158d3478da4d28a1e39323.png)
most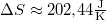 
.
A b) pontban leírt reverzibilis esetben nincs entrópia változás?
![\[ \Delta S=0. \]](/images/math/d/c/8/dc80b86b8504544f66664f9c284be041.png)
Ugyanúgy nincs térfogatváltozás, munkavégzés nem történik (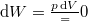, azaz 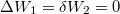), a hőkapacitás az állandó térfogaton mért 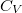hőkapacitás.
![\[ \Delta U = \Delta U_1 + \Delta U_2 = C (T_k-T_1) + C (T_k-T_1) = 2C \left(T_k-\frac{T_1+ T_2} 2\right)=2C\left(\sqrt{T_1 T_2}-\frac{T_1+ T_2} 2\right) \leq 0,\]](/images/math/7/f/9/7f950b6ff90e3ca197363d2338bd5ee7.png)
most 
