„Termodinamika példák - Entrópiaváltozás izoterm táguláskor” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
a (Szöveg koherenssé tétele) |
||
| 10. sor: | 10. sor: | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># $p_1=2\cdot {10}^6\,\mathrm{Pa}$ nyomású, $T=27\,\mathrm{^\circ C}$ hőmérsékletű és $ V_1=1\,\mathrm{l}$ térfogatú ideális gáz izotermikusan $p_2={10}^5\,\mathrm{Pa}$ nyomásig terjed ki. Mennyivel változott meg eközben az entrópiája? | </noinclude><wlatex># $p_1=2\cdot {10}^6\,\mathrm{Pa}$ nyomású, $T=27\,\mathrm{^\circ C}$ hőmérsékletű és $ V_1=1\,\mathrm{l}$ térfogatú ideális gáz izotermikusan $p_2={10}^5\,\mathrm{Pa}$ nyomásig terjed ki. Mennyivel változott meg eközben az entrópiája? | ||
| − | </wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk az entrópiaváltozás definícióját és az állapotegyenletet!}}</wlatex><wlatex>{{Végeredmény|content=$$\Delta S=\frac{p_1 V_1}{T}\ln\frac{p_1}{p_2}$$}}</wlatex></includeonly><noinclude> | + | </wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk az entrópiaváltozás definícióját és az állapotegyenletet!}}</wlatex><wlatex>{{Végeredmény|content=$$\Delta S=\frac{p_1 V_1}{T}\ln\frac{p_1}{p_2}=19{,}97\,\mathrm{\frac{J}{K}}$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| 18. sor: | 18. sor: | ||
$$ \delta Q = \mathrm{d}U+p\,\mathrm{d}V $$ | $$ \delta Q = \mathrm{d}U+p\,\mathrm{d}V $$ | ||
alakját, ahol $ \mathrm{d}U=n C_V\,\mathrm{d}T $ és $ p=\frac{nRT}{V}$: | alakját, ahol $ \mathrm{d}U=n C_V\,\mathrm{d}T $ és $ p=\frac{nRT}{V}$: | ||
| − | $$ \mathrm{d}S= n C_V \frac{\mathrm{d}T}{T} + nR \frac{\mathrm{d}V}{V}. $$ | + | $$ \mathrm{d}S = n C_V \frac{\mathrm{d}T}{T} + nR \frac{\mathrm{d}V}{V}. $$ |
Kiintegrálva az egyenletet $1$ kezdeti- és $2$ végállapot között: | Kiintegrálva az egyenletet $1$ kezdeti- és $2$ végállapot között: | ||
$$ S_2 - S_1 = n C_V \ln\frac{T_2}{T_1} + nR \ln\frac{V_2}{V_1}, $$ | $$ S_2 - S_1 = n C_V \ln\frac{T_2}{T_1} + nR \ln\frac{V_2}{V_1}, $$ | ||
ahol most izotermikusan $T_2=T_1=T$ ($\mathrm{d}T=0$) és $p_i=\frac{nRT}{V_i}$ ($i=1,2$): | ahol most izotermikusan $T_2=T_1=T$ ($\mathrm{d}T=0$) és $p_i=\frac{nRT}{V_i}$ ($i=1,2$): | ||
| − | $$ \Delta S =\frac{p_1 V_1}{T} \ln \frac{p_1}{p_2} | + | $$ \Delta S =\frac{p_1 V_1}{T} \ln \frac{p_1}{p_2}, $$ |
| + | a megadott állapotváltozásra $\Delta S=19{,}97\,\mathrm{\frac{J}{K}}$. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. május 4., 22:56-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Entrópia, II. főtétel |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
-
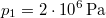nyomású, 
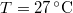hőmérsékletű és 
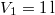térfogatú ideális gáz izotermikusan 
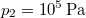nyomásig terjed ki. Mennyivel változott meg eközben az entrópiája?
Megoldás
Az entrópiaváltozás definíciója
![\[ \mathrm{d}S = \frac{\delta Q}{T}, \]](/images/math/c/b/d/cbd5cf7c09169ef24d1244b4e66f68f5.png)
amibe helyettesítsük be a közölt hő első főtételből kifejezett
![\[ \delta Q = \mathrm{d}U+p\,\mathrm{d}V \]](/images/math/f/2/1/f2158c0604f29f1f878df0d5c9709b7f.png)
alakját, ahol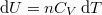 
és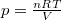 
:
![\[ \mathrm{d}S = n C_V \frac{\mathrm{d}T}{T} + nR \frac{\mathrm{d}V}{V}. \]](/images/math/a/0/b/a0b12548a4cb6f5c634273feb546317b.png)
Kiintegrálva az egyenletet 
kezdeti- és 
végállapot között:
![\[ S_2 - S_1 = n C_V \ln\frac{T_2}{T_1} + nR \ln\frac{V_2}{V_1}, \]](/images/math/d/f/1/df173414052f078a4bc508e9e42cdf8f.png)
ahol most izotermikusan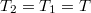 
(
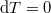) és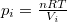 
(
):
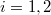![\[ \Delta S =\frac{p_1 V_1}{T} \ln \frac{p_1}{p_2}, \]](/images/math/6/4/8/6481c9b30c460e2a0a7fba30716970e4.png)
a megadott állapotváltozásra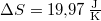 
.
