„Termodinamika példák - Entrópiaváltozás forraláskor” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
a (Szöveg koherenssé tétele) |
||
| 10. sor: | 10. sor: | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># $1\,\mathrm{g}$ $0\,\mathrm{^\circ C}$-os víz állandó nyomáson $100\,\mathrm{^\circ C}$-os gőzzé alakul. Határozzuk meg a folyamat alatt bekövetkező entrópiaváltozást!. | </noinclude><wlatex># $1\,\mathrm{g}$ $0\,\mathrm{^\circ C}$-os víz állandó nyomáson $100\,\mathrm{^\circ C}$-os gőzzé alakul. Határozzuk meg a folyamat alatt bekövetkező entrópiaváltozást!. | ||
| − | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$\Delta S = mc\ln\frac{373}{273}+\frac{ | + | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$\Delta S = mc\ln\frac{373}{273}+\frac{mL_f}{373\,\mathrm{K}}=7{,}36\,\mathrm{\frac{J}{K}},$$ $m=10^{-3}\,\mathrm{kg}$ a víz tömege, $c$ a víz fajhője, $L_f$ a forráshője.}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>Az entrópiát kifejezhetjük az ún. redukált hővel: $\mathrm{d}S=\frac{\delta Q}{T}$, ahol a hőközlést két részre bontjuk. | <wlatex>Az entrópiát kifejezhetjük az ún. redukált hővel: $\mathrm{d}S=\frac{\delta Q}{T}$, ahol a hőközlést két részre bontjuk. | ||
| 16. sor: | 17. sor: | ||
A melegítés során a kezdetben $T_0 = 273\,\mathrm{K}$-es $m=10^{-3}\,\mathrm{kg}$ tömegű víz hőmérséklete folytonosan nő $T_1 = 373\,\mathrm{K}$-re: | A melegítés során a kezdetben $T_0 = 273\,\mathrm{K}$-es $m=10^{-3}\,\mathrm{kg}$ tömegű víz hőmérséklete folytonosan nő $T_1 = 373\,\mathrm{K}$-re: | ||
$$ \Delta S_\text{melegítés} = \int_{T_0}^{T_1}\frac{\delta Q}{T} = cm \int_{T_0}^{T_1} \frac{\mathrm{d}T}{T} = cm \ln \frac{T_1}{T_0}, $$ | $$ \Delta S_\text{melegítés} = \int_{T_0}^{T_1}\frac{\delta Q}{T} = cm \int_{T_0}^{T_1} \frac{\mathrm{d}T}{T} = cm \ln \frac{T_1}{T_0}, $$ | ||
| − | ahol $c= | + | ahol $c=4183\,\mathrm{\frac{J}{kg\,K}}$ a víz fajhője. |
A forralás pedig állandó hőmérsékleten megy végbe, $\delta Q=m L_f$: | A forralás pedig állandó hőmérsékleten megy végbe, $\delta Q=m L_f$: | ||
$$ \Delta S_\text{forralás} = \frac{m L_f}{T_1}, $$ | $$ \Delta S_\text{forralás} = \frac{m L_f}{T_1}, $$ | ||
| − | ahol $L_f=2,26\cdot 10^6\,\mathrm{J}{ | + | ahol $L_f=2{,}26\cdot 10^6\,\mathrm{\frac{J}{kg}}$ a víz forráshője. |
A víz teljes entrópiaváltozása az előző két rész összege: | A víz teljes entrópiaváltozása az előző két rész összege: | ||
| − | $$\Delta S = mc\ln\frac{ | + | $$ \Delta S = mc\ln\frac{T_1}{T_0}+\frac{mL_f}{T_1}, $$ |
| + | $1\,\mathrm{g}$ vízre $\Delta S = 7{,}36\,\mathrm{\frac{J}{K}}$. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. május 12., 23:16-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Entrópia, II. főtétel |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
-
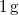
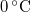-os víz állandó nyomáson 
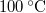-os gőzzé alakul. Határozzuk meg a folyamat alatt bekövetkező entrópiaváltozást!.
Megoldás
Az entrópiát kifejezhetjük az ún. redukált hővel: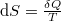 
, ahol a hőközlést két részre bontjuk.
A melegítés során a kezdetben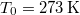 
-es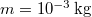 
tömegű víz hőmérséklete folytonosan nő 
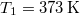-re:
![\[ \Delta S_\text{melegítés} = \int_{T_0}^{T_1}\frac{\delta Q}{T} = cm \int_{T_0}^{T_1} \frac{\mathrm{d}T}{T} = cm \ln \frac{T_1}{T_0}, \]](/images/math/e/e/6/ee6c28f152c4b6ed422652617939a94a.png)
ahol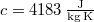 
a víz fajhője.
A forralás pedig állandó hőmérsékleten megy végbe,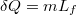 
:
![\[ \Delta S_\text{forralás} = \frac{m L_f}{T_1}, \]](/images/math/c/f/0/cf0e22dcc56ec86e1572af14eedd5170.png)
ahol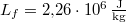 
a víz forráshője.
A víz teljes entrópiaváltozása az előző két rész összege:
![\[ \Delta S = mc\ln\frac{T_1}{T_0}+\frac{mL_f}{T_1}, \]](/images/math/c/e/d/ced7a2c337cc1db1723e9a3cb85db7c8.png)
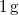vízre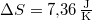 
.
