Munka, energia - 2.2.3

Feladat

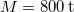1. (2.2.3) Az $\setbox0\hbox{$M=800\,\mathrm{t}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű vasúti szerelvény 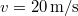$\setbox0\hbox{$v=20\,\mathrm{m/s}$}% \message{//depth:\the\dp0//}% \box0%$ sebességgel halad, amikor leveszik a gőzt. A gördülési súrlódási együttható 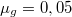$\setbox0\hbox{$\mu_{g}=0,05$}% \message{//depth:\the\dp0//}% \box0%$. Mekkora munkát végez az ellenállási erő a teljes megállásig, és hogyan változik a teljesítménye az időben? Mekkora úton és mennyi idő eltelte után áll meg a szerelvény?

Megoldás

1. Kezdetben a szerelvény teljes kinetikus energiája 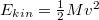$\setbox0\hbox{$E_{kin}=\frac{1}{2}Mv^{2}$}% \message{//depth:\the\dp0//}% \box0%$, amelyet a megállás során teljesen elveszít, így az ellenállás által végzett munka

   $\[W=-\frac{1}{2}Mv^{2}=-1,6\cdot 10^{8} J\,.\]$

   A szerelvény a gördülési ellenállás hatására egyenletesen lassul

   $\[a=\frac{S}{M}=\mu_{g} g\]$

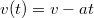   nagyságú gyorsulással. Így a sebesség az idő függvényében $\setbox0\hbox{$v(t)=v-at$}% \message{//depth:\the\dp0//}% \box0%$. A kinetikus energia

   $\[E_{kin}=\frac{1}{2}M(v-at)^{2}\]$

   szerint függ az időtől. Így az ellenállás teljesítménye az idő függvényében

   $\[P(t)=-\frac{dE_{kin}(t)}{dt}=Ma(v-at)\]$

   A teljes megállásig

   $\[T_{stop}=\frac{v}{a}=\frac{v}{\mu_{g}g}=40 \,\mathrm{s}\]$

   telik el. Az ezalatt megtett út

   $\[s=-\frac{W}{S}=\frac{\frac{1}{2}Mv^{2}}{\mu_{g}Mg}=\frac{v^{2}}{2\mu_{g}g}=400\,\mathrm{m}\,.\]$