Munka, energia - 2.3.2
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. október 15., 10:51-kor történt szerkesztése után volt.
Feladat
- (2.3.2) Egy
 tömegű test kezdősebesség nélkül igen nagy
tömegű test kezdősebesség nélkül igen nagy  magasságból esik a Földre. Mekkora a kinetikus energiája a Föld felszínére való becsapódás pillanatában? Mekkora a végsebessége, ha végtelen távolból kezdősebesség nélkül esik a Földre? A légellenállást hanyagoljuk el!
magasságból esik a Földre. Mekkora a kinetikus energiája a Föld felszínére való becsapódás pillanatában? Mekkora a végsebessége, ha végtelen távolból kezdősebesség nélkül esik a Földre? A légellenállást hanyagoljuk el!
Megoldás
- A Föld gravitációs mezejében az
 tömegű test potenciális energiája a Föld középpontjától
tömegű test potenciális energiája a Föld középpontjától![\[V(r)=-\gamma\frac{Mm}{r}\qquad\gamma=6,67\cdot 10^{-11}\,\mathrm{\frac{Nm^{2}}{kg^{2}}}\]](/images/math/3/2/0/3201ce02c7d00c4b7d1f7523cc6be835.png)
 távolságban. A kezdeti állapotban a test távolsága a Föld középpontjától
távolságban. A kezdeti állapotban a test távolsága a Föld középpontjától 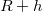 , becsapódáskor pedig
, becsapódáskor pedig  . Ha a légellenállástól eltekintünk, akkor nincs disszipáció, tehát a kezdeti és a végső teljes energia megegyeznek egymással.
. Ha a légellenállástól eltekintünk, akkor nincs disszipáció, tehát a kezdeti és a végső teljes energia megegyeznek egymással. ![\[V(R+h)=V(R)+E_{kin}\qquad\Rightarrow\qquad E_{kin}=\gamma Mm\left(\frac{1}{R}-\frac{1}{R+h}\right)\]](/images/math/5/a/5/5a5b5c6f7d7f9473ec9c9262a496feab.png) Ha végtelen távolból esik a test, vagyis
Ha végtelen távolból esik a test, vagyis![\[E_{kin}=\frac{1}{2}mv^{2}\qquad\Rightarrow\qquad v=\sqrt{\frac{2\gamma Mh}{R(R+h)}}\]](/images/math/1/f/d/1fd23c2cae3a003f330f1fe64b633e90.png)
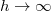 , akkor a test sebessége becsapódáskor.
, akkor a test sebessége becsapódáskor.![\[v=\sqrt{\frac{2\gamma M}{R}}\]](/images/math/c/f/4/cf4ac051639cf85531c2061392214dbd.png)
- A Föld gravitációs mezejében az