Magnetosztatika példák - Félkör alakú vezető darabra ható erő
Feladat
- Egy
 sugarú,
sugarú,  áram által átjárt körvezetőt síkjára merőleges
áram által átjárt körvezetőt síkjára merőleges  indukciójú homogén mágneses térbe helyezünk. Mekkora és milyen irányú erő hat a félkör hosszúságú vezető darabra?
indukciójú homogén mágneses térbe helyezünk. Mekkora és milyen irányú erő hat a félkör hosszúságú vezető darabra?
Megoldás
Tekintsük a körvezető 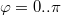 középponti szögekkel jellemzett szakaszát! Ezt felbontjuk infinitezimálisan kis
középponti szögekkel jellemzett szakaszát! Ezt felbontjuk infinitezimálisan kis  szakaszdarabokra, melyekről tudjuk, hogy rájuk:
szakaszdarabokra, melyekről tudjuk, hogy rájuk:
![\[\vec{dF}=I(\vec{dl}\times \vec{B})\]](/images/math/f/5/e/f5e3c0c43a5f70850b8dc9ce5f8c4de7.png)
Lorentz erő hat. Mivel 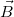 merőleges a körív síkjára, az infinitezimális Lorentz erők mindenütt sugár irányban feszítik a gyűrűt, ha feltételezzük, hogy az
merőleges a körív síkjára, az infinitezimális Lorentz erők mindenütt sugár irányban feszítik a gyűrűt, ha feltételezzük, hogy az  áram az óramutató járásával ellentétes irányban folyik. A félkörívre ható teljes erő ezen elemi erők összegzésével kapható meg. Az
áram az óramutató járásával ellentétes irányban folyik. A félkörívre ható teljes erő ezen elemi erők összegzésével kapható meg. Az  tengelyre szimmetrikus félkör mentén felösszegzett Lorentz erők
tengelyre szimmetrikus félkör mentén felösszegzett Lorentz erők  tengellyel párhuzamos komponensei kioltják egymást, míg az
tengellyel párhuzamos komponensei kioltják egymást, míg az  komponensek konstruktívan adódnak össze. Az elemi Lorentz erő függőleges komponense megkapható a következő módon:
komponensek konstruktívan adódnak össze. Az elemi Lorentz erő függőleges komponense megkapható a következő módon:
![\[dF_y=dF\sin(\varphi)=IB\sin(\varphi)dl\]](/images/math/4/3/d/43d59a7e07ae5178d8e0f749fbbcef70.png)
Az elemi ívdarabok 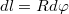 parametrizálásával a következő kifejezést kapjuk az elemi Lorentz erő
parametrizálásával a következő kifejezést kapjuk az elemi Lorentz erő  komponensére:
komponensére:
![\[dF_y=IBR\sin(\varphi)d\varphi\]](/images/math/3/f/c/3fc31c1c56499b73f99d4390adc78325.png)
A teljes félkörívre ható  irányú erőt megkapjuk, ha az elemi
irányú erőt megkapjuk, ha az elemi 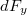 erőket felösszegezzük a
erőket felösszegezzük a 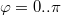 félkörív mentén:
félkörív mentén:
![\[F_y=\int dF_y=IBR \int_0^{\pi} \sin(\varphi)d\varphi=-IBR(\cos(\pi)-\cos(0))=2IBR\]](/images/math/1/9/4/1941b9766799467bd9482f7e768a98bb.png)