Magnetosztatika példák - Szolenoid mágneses tere (Ampere-féle gerjesztés)
Feladat
- Határozzuk meg a mágneses indukció nagyságát egy
 hosszúságú,
hosszúságú,  menetű szolenoidban, amelyben
menetű szolenoidban, amelyben  áram folyik gerjesztési törvény segítségével.
áram folyik gerjesztési törvény segítségével.
Megoldás
a.) Vegyünk fel egy 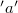
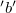
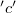
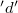 oldalakkal határolt téglalap alakú zárt hurkot, melynek
oldalakkal határolt téglalap alakú zárt hurkot, melynek 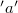 oldala
oldala  hosszúságú, és egybe esik a szolenoid tengelyével. Az erre merőleges
hosszúságú, és egybe esik a szolenoid tengelyével. Az erre merőleges 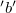 és
és 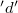 oldalai igen hosszúak, így a téglalap szintén
oldalai igen hosszúak, így a téglalap szintén  hosszúságú
hosszúságú 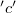 oldala olyan távol van a szolenoidtól, hogy annak tere ott már elhanyagolható.
Írjuk fel erre a zárt görbére az Amper-féle gerjesztési törvényt:
oldala olyan távol van a szolenoidtól, hogy annak tere ott már elhanyagolható.
Írjuk fel erre a zárt görbére az Amper-féle gerjesztési törvényt:
![\[\sum I=\oint \vec{H}\vec{dl}\]](/images/math/6/a/a/6aaa8b49e2de5a331efe6620c4dfcc74.png)
A zárt görbe által határolt területen átfolyik a szolenoid  darab menetének
darab menetének  árama, így a gerjesztési törvény:
árama, így a gerjesztési törvény:
![\[NI=\int_a \vec{H}\vec{dl}+\int_b \vec{H}\vec{dl}+\int_c \vec{H}\vec{dl}+\int_d \vec{H}\vec{dl}\]](/images/math/4/a/e/4ae37ef2c2ce3bbc77129fcd75373b2b.png)
Vegyük szemügyre a zárt görbére vonatkozó integrált. A téglalap alakú görbe  hosszúságú, a szolenoid tengelyével egybeeső
hosszúságú, a szolenoid tengelyével egybeeső 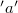 oldala mentén feltételezzük, hogy a
oldala mentén feltételezzük, hogy a  térerősség állandó nagyságú, mely feltételezés helytálló, ha a szolenoid nagyságrendekkel hosszabb, mint a tekercs átmérője. A tekercs hengerszimmetriája miatt feltételezhetjük azt is, hogy a
térerősség állandó nagyságú, mely feltételezés helytálló, ha a szolenoid nagyságrendekkel hosszabb, mint a tekercs átmérője. A tekercs hengerszimmetriája miatt feltételezhetjük azt is, hogy a 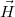 térerősség vektor a tekercs tengelye mentén mindenütt tengelyirányú. Ezen feltételezések mellett az általunk felvett téglalap szolenoidban futó
térerősség vektor a tekercs tengelye mentén mindenütt tengelyirányú. Ezen feltételezések mellett az általunk felvett téglalap szolenoidban futó 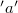 oldala mentén a gerjesztési törvényben szereplő integrál az alábbiak szerint egyszerűsödik:
oldala mentén a gerjesztési törvényben szereplő integrál az alábbiak szerint egyszerűsödik:
![\[\int_a \vec{H}\vec{dl}=H\int_a dl=Hl\]](/images/math/f/c/8/fc8661c1e8617a3f6ad65b8d032eb66f.png)
A szolenoid geometriája miatt feltételezhetjük, hogy a tekercs két végén kifutó mágneses erővonalak profiljai egymásra tükörszimmetrikusak, csak az erővonalakat alkotó vektorok mutatnak az egyik végen a tekercs belseje felé, míg a másik végen kifelé. ezen szimmetriatulajdonság miatt feltételezzük, hogy az általunk felvett téglalap tekercs tengelyére merőleges oldalai mentén kiszámított integrálok egymásnak ellentettjei:
![\[\int_d \vec{H}\vec{dl}=-\int_b \vec{H}\vec{dl}\]](/images/math/a/f/8/af87df5b8622e2ce4691d9da765e7fa7.png)
A téglalap 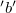 és
és 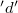 oldalát elegendően hosszúra választva az utolsó,
oldalát elegendően hosszúra választva az utolsó, 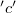 oldal olyan távol esik a szolenoidtól, hogy ott a szolenoid tere elhanyagolható
oldal olyan távol esik a szolenoidtól, hogy ott a szolenoid tere elhanyagolható 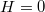 . Így a
. Így a 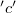 oldalra vett integrál értéke is zérus:
oldalra vett integrál értéke is zérus:
![\[\int_c \vec{H}\vec{dl}=0\]](/images/math/9/c/3/9c3156d656736a7f6de2eebb7c1bc385.png)
Ezen közelítéseknek köszönhetően a gerjesztési törvény tovább egyszerűsíthető:
![\[NI=\int_a \vec{H}\vec{dl}+\int_b \vec{H}\vec{dl}+\int_c \vec{H}\vec{dl}+\int_d \vec{H}\vec{dl}=Hl+\int_b \vec{H}\vec{dl}-\int_b \vec{H}\vec{dl}+0\]](/images/math/3/7/6/3768c8794ef0e83100be87cec5fb8fd5.png)
A kapott egyenlet:
![\[NI=Hl\]](/images/math/4/3/f/43f3d606ba460d88eac0b42383c61106.png)
Ebből kiszámolható az  árammal átjárt
árammal átjárt  hosszúságú szolenoid belsejében mérhető mágneses indukció:
hosszúságú szolenoid belsejében mérhető mágneses indukció:
![\[B=\dfrac{\mu_0 NI}{l}\]](/images/math/2/0/7/207641385b12448b0305980157b8c127.png)