Magnetosztatika példák - Légrésben és a vasmagban tárolt energia

Feladat

1. Egy $\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%$ középsugarú, $\setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0%$ keresztmetszetű vasgyűrűre $\setbox0\hbox{$N$}% \message{//depth:\the\dp0//}% \box0%$ menetet tekercselnek. A gyűrűn $\setbox0\hbox{$b$}% \message{//depth:\the\dp0//}% \box0%$ széles légrést alakítanak ki. A használatos gerjesztő áramoknál a vas relatív permeabilitása $\setbox0\hbox{$\epsilon_r$}% \message{//depth:\the\dp0//}% \box0%$. 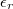Határozzuk meg a légrésben és a vasmagban tárolt energia arányát! Az energiából mekkora öninduktivitás számolható?

Megoldás

Írjuk fel az Ampére-féle gerjesztési törvényt egy, a toroid belsejében elhelyezkedő körre, melynek tengelye a toroid forgástengelyével egybe esik:

$\[\oint \vec{H}\vec{dl} = NI\]$

A mágneses tér az egyes közegekben állandó nagyságú, érintő irányú.

$\[H_{vas}(2\pi r-b)+H_{res} b = N I\]$

Mivel a mágneses indukció mindkét közegben egyforma, ezért:

$\[\frac{B}{\mu_0 \mu_r} (2\pi r-b) + \frac{B}{\mu_0} b = NI \]$

Ebből a mágneses indukció mindkét közegben:

$\[B = \frac{NI\mu_0} {\left(\frac{2\pi r-b}{\mu_r}+b \right)} \]$

A mágneses térerősség a két közegben:

$\[H_{vas} = \frac{B}{\mu_0 \mu_r} = \frac{NI}{\mu_r \left(\frac{2\pi r-b}{\mu_r}+b\right)}\]$

$\[H_{res} = \frac{B}{\mu_0} = \frac{NI}{ \left(\frac{2\pi r-b}{\mu_r}+b\right)}\]$

A vasmagban és a légtésben tárolt energiát úgy határozhatjuk meg, ha kiszámoljuk mindkét térrészben az energiasűrűséget (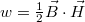$\setbox0\hbox{$w = \frac{1}{2}\vec{B}\cdot\vec{H}$}% \message{//depth:\the\dp0//}% \box0%$), és azt megszorozzuk térrész térfogatával.Ezzel a légrésben tárolt energia:

$\[E_{leg} = \frac{1}{2} \frac{N^2I^2\mu_0} {\left( \frac{2\pi r-b}{\mu_r}+b\right)^2} \cdot V_{leg} =\frac{1}{2} \frac{N^2I^2\mu_0} {\left(\frac{2\pi r-b}{\mu_r}+b\right)^2}\cdot Ab \]$

A vasmagban pedig:

$\[E_{vas} = \frac{1}{2} \frac{N^2I^2\mu_0 } {\mu_r \left( \frac{2\pi r-b}{\mu_r}+b\right)^2} \cdot V_{vas} =\frac{1}{2} \frac{N^2I^2\mu_0 } {\mu_r \left(\frac{2\pi r-b}{\mu_r}+b\right)^2}\cdot A(2\pi r-b) \]$

Ebből a légrésben és a vasmagban tárolt enerigia aránya:

$\[\frac{E_{leg}}{E_{vas}} = \frac{b}{\mu_r\left(2\pi r-b\right)}\]$

Mivel a tekercsre igaz hogy:

$\[E = \frac{1}{2}LI^2\]$

Ezért az energiából a következőképpen számolhatjuk ki az öninduktivitást:

$\[L = \frac{2 \left( E_{vas}+E_{leg} \right)} {I^2}\]$