4. Rezgések
A harmonikus oszcillátor a fizika egyik állatorvosi lova, hiszen egy elméletileg egyszerűen tárgyalható modellt szolgáltat, mely számos gyakorlati jelenséget nagy pontossággal leír. Mechanikai rezgésekkel találkozhatunk többek között hangszerek működésénél, hidak rezonancia-katasztrófáinál, a kvarc órák alapját képező oszcillátoroknál, vagy atomi pontosságú méréseket lehetővé tevő atomi erő mikroszkópban. A modell egyszerű ismertetése után számos technikai alkalmazáson keresztül szemléltetjük a rezonancia, csillapítás, jósági tényező gyakorlati jelentőségét.
A harmonikus oszcillátor jó példa a lineáris rendszerekre, ahol a „visszatérítő” hatás a „kitéréssel” arányos. Gyakran előfordul azonban az is, hogy a rendszer az egyensúlyi helyzetétől „igen távoli” állapotba kerül és a visszatérítő hatások már nem lineárisak. Ekkor a rendszer mozgása „kaotikus” lesz, annak ellenére, hogy a mozgástörvények jól ismertek. A kaotikus mozgás természetét a kaotikus kettős inga példáján keresztül szemléltetjük.
Végül a rezgések térbeli terjedésének, a hullámoknak a fizikáját ismertetjük. A mechanikai hullámok gyakorlati jelentősége jól szemléltethető az orvosi ultrahangos diagnosztika tökéletességig fejlesztett elvein keresztül.
A mechanikai rezgések és hullámok fizikája nem utolsó sorban fontos alap az elektromosságtan és kvantummechanika számos fejezetének tárgyalásához.
Tartalomjegyzék[elrejtés] |
Rezgések és hullámok
Rezgések és hullámok a természetben
A rezgések és a hullámok a természet alapvető mozgásformái. Rezgésekkel és hullámokkal nem csak a mechanikában, hanem a fizika minden más területén (pl. elektromos rezgőkörök, optika, kvantummechanika), a többi természettudományokban (pl. meteorológiai és kémiai és biológiai oszcillációk), sőt a társadalomtudományokban is (pl. gazdasági ciklusok) találkozunk.
Itt elsősorban mechanikai rezgésekkel és hullámokkal foglalkozunk (de utalunk pl. a mechanikai és elektromos rezgések közti analógiára). A rezgés természetes mozgás: a környezetünkben szinte minden test végez rezgőmozgást az atomi méretektől az égitestekben kialakuló rezgésekig. A kvarckristály rezgésén alapul az órák működése. A hangszerek pedig húrok, rugalmas felületek és légoszlopok rezgésével kelt hangot. A gépek, épületek túlzott rezgései komoly veszélyt jelenthetnek, amit el kell kerülni, hintázásnál viszont éppen az a cél, hogy minél nagyobb amplitúdójú rezgés jöjjön létre. A mechanikai hullámok közül a folyadékok felszínén kialakuló hullámok jól láthatók és megfigyelhetők, amik segítik más hullámjelenségek, mint például a hang megértését.
A mechanikai rezgés egy rendszer egyensúlyi helyzet körüli, időben többé-kevésbé periodikus mozgása. A rezgések közül elméleti és gyakorlati szempontból is kiemelkedő fontosságú a harmonikus rezgőmozgás, ahol a kitérés időfüggvénye harmonikus (szinuszos vagy koszinuszos) függvény.
A mechanikai hullámok egy rugalmas közegben jöhetnek létre valamilyen „zavar” tovaterjedésével. A hullámok térben és időben is periodikus jelenségek, több olyan jellegzetes viselkedést is mutatnak, amelyek csak a hullámokra jellemzők (például az interferencia).
A legegyszerűbb lineáris rendszer
A harmonikusan gerjesztett, csillapított mechanikai oszcillátor
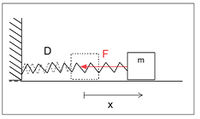
A rugalmas testekben nem túl nagy deformáció hatására a deformációval ellentétes irányú, azzal arányos erő lép fel:![\[\vec{F}=-D\vec{r}\]](/images/math/0/3/9/039ee317de88bd442ee59b27bda1bb1d.png)
 -tengely irányú kitérés esetén):
-tengely irányú kitérés esetén): ![\[ma=-Dx\]](/images/math/f/b/3/fb30b4da9009aab1cbabab9dff6513fa.png)
![\[a=\frac{{\rm d}^2x}{{\rm d}t^2}=\ddot{x}\]](/images/math/5/3/1/531c0e3f0ef1d47c0c4899356fe8f85c.png)
![\[\frac{D}{m}=\omega_0^2\]](/images/math/6/3/b/63beca5b476fb96e981556e2765b9e7a.png)
![\[\ddot{x}+\omega_0^2x=0\]](/images/math/b/7/6/b76d01932fe1162cb76d9b143578f817.png)
![\[x(t)=A\sin\left(\omega_0t+\varphi_0\right)\]](/images/math/3/5/0/350c6aaa0288df90f46d0af2ae539461.png)
 saját-körfrekvenciát a rendszer fizikai paramétereitől függ. Az
saját-körfrekvenciát a rendszer fizikai paramétereitől függ. Az  amplitúdót (maximális kitérés) és a
amplitúdót (maximális kitérés) és a 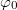 kezdőfázist viszont a kezdeti feltételek határozzák meg. Az
kezdőfázist viszont a kezdeti feltételek határozzák meg. Az  saját-körfrekvencia helyett gyakran használatos az
saját-körfrekvencia helyett gyakran használatos az ![\[f_0=\frac{\omega_0}{2\pi}\]](/images/math/6/6/b/66b01055bfdba6447d0738d571d13a77.png)
![\[T_0=\frac{1}{f_0}=\frac{2\pi}{\omega_0}\]](/images/math/4/f/d/4fdeb60d1d02ce3bb97ac6b5f62e4b71.png)
![\[F_{cs}=-kv\]](/images/math/0/1/5/0158b563a1c2686245d41447480081f5.png)
![\[v=\frac{{\rm d}x}{{\rm d}t}=\dot{x}\]](/images/math/6/3/f/63f5cc3f6fe77bd2391f6fe985594620.png)
![\[\frac{k}{m}=2\beta\]](/images/math/4/7/4/47409373dc7f76a069177bb0f62a17b3.png)
![\[\ddot{x}+2\beta\dot{x}+\omega_0^2x=0\]](/images/math/8/5/2/8529bfb04c4d37981de667e07b18cb7e.png)
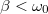 ) csillapítás esetén:
) csillapítás esetén: ![\[x(t)=A e^{-\beta t}\sin\left(\omega ' t+\varphi_0\right)\]](/images/math/5/c/8/5c8750e646f4ae2d71189949b79e54d3.png)
 a korábban definiált csillapítási tényező, és
a korábban definiált csillapítási tényező, és ![\[\omega ' =\sqrt{\omega_0^2-\beta^2}\]](/images/math/4/8/7/4872c74123c7d0a829f26855c6f78317.png)
 és
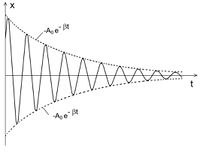
és 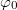 most is a kezdeti feltételektől függenek. A mozgás egy olyan rezgés, melynek amplitúdója az idővel exponenciálisan csökken (2. ábra). A megoldás helyességéről behelyettesítéssel ismét meg lehet győződni.
most is a kezdeti feltételektől függenek. A mozgás egy olyan rezgés, melynek amplitúdója az idővel exponenciálisan csökken (2. ábra). A megoldás helyességéről behelyettesítéssel ismét meg lehet győződni.
![\[F(t)=F_0\sin(\omega t)\]](/images/math/9/2/c/92c3dd03ece36d308583fe8d0bf9a29d.png)
![\[f_0=\frac{F_0}{m}\]](/images/math/b/c/7/bc73de2c71174531c377eb898d382c67.png)
![\[\ddot{x}+2\beta\dot{x}+\omega_0^2x=f_0\sin(\omega t)\]](/images/math/b/c/b/bcbe13180796f38c207b74d5cd062635.png)
A mozgásegyenlet analitikus megoldása
A mozgásegyenlet egy másodrendű inhomogén lineáris differenciálegyenlet. Ennek megoldása két tagból áll: Az egyik a homogén egyenlet megoldása, azaz a nem gerjesztett csillapított rezgés. Ez a tag az indítás után exponenciálisan elhal, ezért átmeneti, tranziens tagnak nevezzük:![\[x_1(t)=A_t e^{-\beta t}\sin\left(\omega ' t+\varphi_0\right)\]](/images/math/1/2/c/12cfcc8323b0271f7de65f34a97a0984.png)
 (a gerjesztés körfrekvenciájával megegyező) körfrekvenciájú harmonikus rezgés. Ennek amplitúdója és a gerjesztéshez viszonyított fáziseltolódása függ a gerjesztés körfrekvenciájától, a rezgés saját-körfrekvenciájától és a csillapítási tényezőtől:
(a gerjesztés körfrekvenciájával megegyező) körfrekvenciájú harmonikus rezgés. Ennek amplitúdója és a gerjesztéshez viszonyított fáziseltolódása függ a gerjesztés körfrekvenciájától, a rezgés saját-körfrekvenciájától és a csillapítási tényezőtől: ![\[x_2(t)=A\sin(\omega t+\varphi)\]](/images/math/6/0/0/600e4eaf978160a490b0f985719f8247.png)
![\[A=\frac{f_0}{\sqrt{\left(\omega_0^2-\omega^2\right)+4\beta^2\omega^2}}\]](/images/math/9/d/3/9d394380ee6cfd3d9e091dd454249301.png)
![\[\varphi=\arctan\frac{2\beta\omega}{\omega_0^2-\omega^2}\]](/images/math/3/6/7/3671aabcc1d8fa97d4265e2f1665fdf2.png)
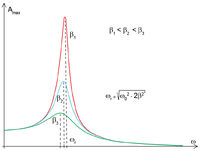
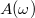 amplitúdóját a gerjesztés körfrekvenciájának függvényében, akkor – különböző csillapításokkal – a 3. ábrán látható görbesereget kapjuk. A görbéknek maximuma van az
amplitúdóját a gerjesztés körfrekvenciájának függvényében, akkor – különböző csillapításokkal – a 3. ábrán látható görbesereget kapjuk. A görbéknek maximuma van az ![\[\omega_{max}=\sqrt{\omega_0^2-2\beta^2}\]](/images/math/9/1/5/915a5a394448e94f7f6df72c7607febb.png)
![\[A_{max}=\frac{f_0}{2\beta\sqrt{\omega_0^2-2\beta^2}}\approx\frac{f_0}{2\beta\omega_0}\qquad({\rm ha}\quad\beta^2\ll\omega_0^2)\]](/images/math/2/9/6/2968dde3500ed6bcbf60365f0377845b.png)
 csökkenésével a maximális amplitúdó növekszik. Ez a rezonancia jelensége. A rezonanciagörbe élességét szokás a
csökkenésével a maximális amplitúdó növekszik. Ez a rezonancia jelensége. A rezonanciagörbe élességét szokás a  jósági tényezővel jellemezni.
jósági tényezővel jellemezni. ![\[Q=\frac{\omega_0}{2\beta}\]](/images/math/7/8/b/78b30bf0910c86b931f5fddbb6fad70c.png)
Minél kisebb a csillapítás, annál nagyobb a jósági tényező.
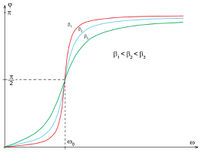
A 4. ábrán az állandósult rezgés és a gerjesztés közti 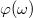 fáziseltolódás látható a gerjesztés körfrekvenciájának függvényében. Látható, hogy kis (
fáziseltolódás látható a gerjesztés körfrekvenciájának függvényében. Látható, hogy kis (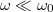 ) gerjesztő frekvenciánál a rezgő test szinte fáziskésés nélkül követi a kényszert, a körfrekvencia növelésével viszont egyre inkább késik hozzá képest.
) gerjesztő frekvenciánál a rezgő test szinte fáziskésés nélkül követi a kényszert, a körfrekvencia növelésével viszont egyre inkább késik hozzá képest. 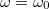 frekvenciánál a fáziskésés
frekvenciánál a fáziskésés 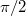 , nagyon nagy frekvenciáknál pedig már
, nagyon nagy frekvenciáknál pedig már 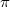 , azaz a rezgő test a kényszerrel ellentétes fázisban rezeg.
, azaz a rezgő test a kényszerrel ellentétes fázisban rezeg.
![\[x(t)=A_t e^{-\beta t}\sin\left(\omega ' t+\varphi_0\right)+\frac{f_0}{\sqrt{\left(\omega_0^2-\omega^2\right)+4\beta^2\omega^2}}\sin(\omega t+\varphi)\]](/images/math/c/9/2/c92f4276aeb76698bc50437b5996ed28.png)
A megoldás helyességéről ebben az esetben is a differenciálegyenletbe való behelyettesítéssel lehet meggyőződni.
A különböző rezgések megértéséhez segítséget nyújtanak a számítógépes szimulációk. Az alábbi videók MATLAB programnyelvvel készült szimulációkat szemléltetnek. A szimulációk leírása és forráskódja a Matlab szimulációk oldalon található meg.
| Csillapított rezgés Részletesen |
Gerjesztett rezgés Részletesen |
Csatolt rezgés Részletesen |
Rezgések összetevése Részletesen |
Rezgések összetevése Részletesen |
A lineáris rendszerek analízisének alapjai
Dirac-delta és ugrás-függvény gerjesztés
Lineáris rendszerek a fizika és a technika számos területén előfordulnak. Fontos szerepet kapnak például a jelfeldolgozás és az irányítástechnika elméletében. A villamosmérnöki gyakorlatból ismert lineáris rendszerek az ellenállásokból, kondenzátorokból és tekercsekből álló lineáris hálózatok (a harmonikusan gerjesztett, csillapított mechanikai oszcillátorral analóg soros RLC-rezgőkör viselkedését részletesebben megvizsgáljuk).
A lineáris rendszereket lineáris differenciálegyenlet-rendszerek írják le. Ezek megoldása tetszőleges gerjesztés esetén (különösen összetettebb, sokváltozós rendszereknél) nem könnyű. Sokszor nincs is szükség ismerni a rendszer összes változóját az idő függvényében, elég valamely számunkra fontos mennyiség időfüggése. Ez a válaszfüggvény természetesen függ a gerjesztéstől.
A lineáris rendszerek legfontosabb tulajdonsága, hogy teljesül a szuperpozíció elve: ha két gerjesztés összege hat a rendszerre, akkor a válasz az egyes gerjesztésekre adott válaszok összege lesz. Emiatt egy lineáris rendszer egyértelműen jellemezhető egyetlen – célszerűen egyszerű – gerjesztésre adott válasszal is. Ez a válaszfüggvény megmérhető vagy kiszámítható, és ismeretében már bármely gerjesztésre adott válasz meghatározható.
A lineáris rendszerek vizsgálatára használt legegyszerűbb gerjesztések a Dirac-delta függvény és az egységugrás függvény.
A Dirac-delta függvény definíciója:![\[\delta(t)=\begin{cases}\infty &{\rm ha}\quad t=0\\0 &{\rm ha}\quad t\ne 0\end{cases}\]](/images/math/b/c/7/bc76807f82feba20de993d3e5a008cf1.png)
![\[\int_{-\infty}^{+\infty}\delta(t){\rm d}t=1\]](/images/math/4/e/b/4ebe0efd50cffa51b6ca26c6eaf9412a.png)
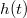 súlyfüggvény ismeretében tetszőleges
súlyfüggvény ismeretében tetszőleges 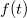 gerjesztésre adott
gerjesztésre adott 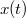 válasz meghatározható: a gerjesztő függvény időben eltolt, változó nagyságú impulzusok összegeként (integráljaként) fogható fel.
válasz meghatározható: a gerjesztő függvény időben eltolt, változó nagyságú impulzusok összegeként (integráljaként) fogható fel. ![\[x(t)=\int_{-\infty}^t f(\tau)h(t-\tau){\rm d}\tau=f(t)*h(t)\]](/images/math/0/8/d/08d826746887363cd2dc150128ad5d7b.png)
ahol  a konvolúció jele.
a konvolúció jele.
![\[\varepsilon(t)=\begin{cases}0 &{\rm ha}\quad x<0\\1 &{\rm ha}\quad x>0\end{cases}\]](/images/math/e/b/f/ebf89acf2174d191d8e5377c80648792.png)
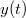 átmeneti függvény segítségével is megadható, ekkor a gerjesztést időben eltolva belépő kicsiny ugrások szuperpozíciójaként fogjuk fel:
átmeneti függvény segítségével is megadható, ekkor a gerjesztést időben eltolva belépő kicsiny ugrások szuperpozíciójaként fogjuk fel: ![\[x(t)=f(0)y(t)+\int_0^t\frac{{\rm d}f(\tau)}{{\rm d}\tau}y(t-\tau){\rm d}\tau=f(0)y(t)+\dot{f}(t)*y(t)\]](/images/math/f/a/4/fa4e3d5360c435b457dfc5f8231b5e85.png)
Kísérlettek: különböző gerjesztések és csillapítások
A videón látható kísérletben a szinuszos gerjesztés frekvenciája folyamatosan változik. Megfigyelhető, hogy a rezgő test kitérése a rezonanciafrekvencia közelében maximális (rezonancia).
Egy másik videón egy bonyolultabb, több szabadsági fokú rendszer viselkedése látható. Egy ilyen rendszernek több rezonanciafrekvenciája van.
A gerjesztés jellegének, a gerjesztés frekvenciájának és a csillapításnak a hatása még jobban megfigyelhető a Pohl-féle készülék segítségével. Ebben a kísérletben jól tanulmányozható a szinuszos gerjesztés és a rezgés közötti fáziskülönbség is. Ez a kísérlet bemutatásra kerül az előadáson.
Rezonancia: a hintázástól a rezonanciakatasztrófáig
Rezonancia akkor lép fel egy gerjesztett rezgésnél, ha a kényszer frekvenciája közel van a rendszer sajátfrekvenciájához, és a csillapítás nem túl nagy (lásd a videót).
A rezonancia jelenségével már egészen kis korában találkozik mindenki: ha hintázás közben össze-vissza lökjük, vagy hajtjuk a hintát, akkor alig fog mozogni – ha viszont megfelelő ritmusban, akkor a hinta egyre nagyobb amplitúdóval fog lengeni.
A rezonancia jelenségével az élet minden területén találkozhatunk.
Mechanikai rezonancia az alapja a zenei (és az emberi) hang létrejöttének: húrok, felületek, légoszlopok a gerjesztés (pengetés, vonó, ütés, fújás, stb.) hatására meghatározott frekvenciákon fognak nagy amplitúdóval rezegni. Ezek a frekvenciák a rezgő rendszer (húr, felület, légoszlop) sajátfrekvenciái, melyek általában egy alapfrekvencia egészszámú többszörösei (az ún. felharmonikusok). A hang magasságát az alapfrekvencia értéke határozza meg, a hangszínt pedig a felharmonikusok aránya.
Az időmérés, az órák működése szintén a rezonancia jelenségére épül: az ingaórák ingájának, a hagyományos karórák torziós rezgést végző lengőkerekének, a kvarcórák kvarckristályának periódusideje határozza meg azt az elemi időtartamot, aminek számlálásával az óra az időt méri.
A lézer működésének alapja az optikai rezonancia: a lézer tükreinek távolsága úgy van beállítva, hogy a többszörös visszaverődés erősítse a fényt. Az erősítés csak egy meghatározott frekvencián jön létre, ez is oka annak, hogy a lézerfény nagyon jó közelítéssel monokromatikus (egyszínű).
A mikrohullámú sütőben szintén szerepet kap a rezonancia: a sütő fémdoboza egy rezonáns üreg a mikrohullámok számára. Ugyanakkor nem igaz, hogy a sütőben alkalmazott elektromágneses sugárzás frekvenciája (2,45 GHz) megegyezne a vízmolekulák valamely sajátfrekvenciájával (a legalacsonyabb saját frekvencia is egy nagyságrenddel magasabb). A víz azért melegszik jobban a sütőben, mint az üveg, a porcelán vagy a műanyagok, mert a vízmolekulák erősen polárosak, és az elektromágneses tér hatására ide-oda forognak, ami melegedést okoz.
Az atomok és molekulák rezonanciáját számos kísérleti technika használja. Ilyen például az orvosi diagnosztikában is használt mágneses magrezonancia (MRI). A vizsgálattal a testben lévő hidrogénatomok eloszlása térképezhető fel három dimenzióban akár tizedmilliméteres felbontással. (Ebből pedig a különböző szövetek térbeli elhelyezkedésére és működésére lehet következtetni.)
A rezonancia segítségével lehet különböző frekvenciájú rezgések közül egy meghatározott frekvenciájú rezgést felerősíteni és kiválasztani. Ez teszi lehetővé a hangmagasság érzékelését a fülünkben és a rádióhullámok szelektív vételét a rádiótól a mobiltelefonig minden vezeték nélküli eszközben. A fülben a különböző magasságú hangokra a belső fül más-más része rezonál, és így a hang más idegsejtet ingerel, lehetővé téve ezzel a hangok hangmagasság (és a hangszín) szerinti megkülönböztetését. A rádióban az állomáskereső gomb a vevő elektromos rezgőkörét hangolja a kívánt adó frekvenciájára, lehetővé téve ezzel egyetlen adás kiválasztását az antennát érő rengeteg rádióhullám közül. Minél nagyobb a rádió rezgőkörének jósági tényezője, annál jobban szét tud választani egymáshoz közeli adókat. A mobiltelefonban vagy a GPS-ben szintén nagyon pontosan hangolt rezonátorok teszik lehetővé az adótornyok, illetve a műholdak által sugárzott rádióhullámok vételét.
Ugyanakkor a rezonancia veszélyes is lehet: kis csillapítású rendszerek kis intenzitású gerjesztés hatására is veszélyesen nagy amplitúdójú rezgést végezhetnek, ha a gerjesztés frekvenciája a rezonanciafrekvencia közelébe esik. Az egyre nagyobb amplitúdójú rezgés a rezgő rendszert felépítő elemek töréséhez, szakadásához vezethet: ez a rezonanciakatasztrófa jelensége.
A középkorban a nagy templomkupolák építésénél figyelték meg, hogy a kupola széllökések hatására berezonálhat és összedőlhet. Ez ellen úgy tudtak védekezni, hogy a kupolát megduplázták: két, különböző sugarú gömbhéjból építették meg. Ha a két héj rezonanciafrekvenciája jelentősen eltér egymástól, akkor kölcsönösen csillapítani képesek egymás rezgéseit, hiszen egyszerre csak az egyik kerülhet rezonanciahelyzetbe.
Az egyik leghíresebb rezonanciakatasztrófa a Tacoma-híd leszakadása volt. A híd tervezésekor nem számoltak azzal, hogy a szél hatására olyan örvények keletkezhetnek a híd mögött, melyek frekvenciája közel esik a híd egyik sajátfrekvenciájához. Ennek hatására a híd torziós (csavarodó) rezgésbe kezdett, melynek amplitúdója addig növekedett, míg végül a híd leszakadt. A híd rezonanciájáról és leszakadásáról film is készült, amelyen a leszakadáshoz vezető folyamat jól megfigyelhető.
Analógia a gerjesztett, csillapított elektromos rezgőkörrel
Érdemes részletesebben is megvizsgálni a harmonikusan gerjesztett, csillapított mechanikai oszcillátor és egy elektromos rezgőkör (soros RLC-kör) közti analógiát.
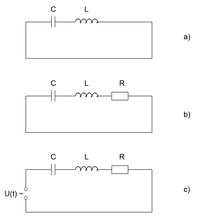
Egy kondenzátorból és egy tekercsből (5/a ábra) olyan rezgő rendszer készíthető, amelynek viselkedése az 1. ábrán látható csillapítatlan mechanikai oszcillátorhoz hasonlít. Felírva a kondenzátor és a tekercs egyenleteit![\[I_C=C\frac{{\rm d}U_C}{{\rm d}t}=C\dot{U}_C\]](/images/math/a/3/e/a3e3ad63215d0de4923d5ee88f7dcedf.png)
![\[U_L=L\frac{{\rm d}I_L}{{\rm d}t}=L\dot{I}_L\]](/images/math/c/5/1/c51e83ca66cca19d6bc56e46cae610d6.png)
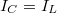 és
és 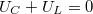 , és rendezve az egyenleteket:
, és rendezve az egyenleteket: ![\[U_C=-U_L=-L\dot{I}_L=-L\dot{I}_C=-LC\ddot{U}_C\]](/images/math/8/d/e/8de7d350909193283f7fac426632e59f.png)
![\[\frac{1}{LC}=\omega_0^2\]](/images/math/7/2/f/72f0502b1d655a280276ba169003d346.png)
![\[\ddot{U}_C+\omega_0^2U_C=0\]](/images/math/7/4/b/74ba1df4cef8650f6a20843fb600e1a7.png)
![\[U_C(t)=\widehat{U}_C\sin(\omega_0t+\varphi_0)\]](/images/math/5/5/5/555f433fe17e9c4105d10e0e67436431.png)
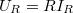 , a Kirchhoff-törvények (a pillanatértékekre):
, a Kirchhoff-törvények (a pillanatértékekre): 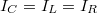 és
és 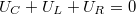 . Behelyettesítve és rendezve látható, hogy a csillapított rezgőkörnek a differenciálegyenlete a csillapított mechanikai oszcillátoréval analóg:
. Behelyettesítve és rendezve látható, hogy a csillapított rezgőkörnek a differenciálegyenlete a csillapított mechanikai oszcillátoréval analóg: ![\[\ddot{U}_C+\frac{R}{L}\dot{U}_C+\frac{1}{LC}U_C=0\]](/images/math/4/1/e/41ec94b7e3da2c78d47d332803f9cfb8.png)
![\[U_C(t)=\widehat{U}_Ce^{-\beta t}\sin(\omega ' t+\varphi_0)\]](/images/math/6/e/6/6e62bee33fb5dcac552f0cd6a0808916.png)
![\[\beta=\frac{R}{2L}\qquad\omega '=\sqrt{\omega_0^2-\beta^2}\]](/images/math/e/4/5/e452f93d76e5def8f47c01f2e27f7f53.png)
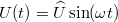 alakú harmonikus gerjesztés esetén a differenciálegyenlet
alakú harmonikus gerjesztés esetén a differenciálegyenlet ![\[\ddot{U}_C+\frac{R}{L}\dot{U}_C+\frac{1}{LC}U_C=u\sin(\omega t)\]](/images/math/7/1/e/71ee6232d011cd09dd36161e9173c082.png)
![\[u=\frac{\widehat{U}}{LC}\]](/images/math/b/6/2/b62150c330f25b200f7eb621b70aad4d.png)
![\[U_C(t)=U_t e^{-\beta t}\sin\left(\omega ' t+\varphi_0\right)+\frac{u_0}{\sqrt{\left(\omega_0^2-\omega^2\right)+4\beta^2\omega^2}}\sin(\omega t+\varphi)\]](/images/math/e/f/1/ef155c15bd28842d8877b0fa86319cd1.png)
![\[\widehat{U}_C=\frac{u_0}{\sqrt{\left(\omega_0^2-\omega^2\right)^2+4\beta^2\omega^2}}=\frac{\widehat{U}_0}{LC\sqrt{\left(\frac{1}{LC}-\omega^2\right)^2+4\left(\frac{R}{2L}\right)^2\omega^2}}=\frac{\widehat{U}_0}{C\omega\sqrt{\left(\frac{1}{C\omega}-L\omega\right)^2+R^2}}=\frac{X_C}{Z}\widehat{U}_0\]](/images/math/0/5/7/057c0c9af8bce1a91d123948fe1fecce.png)
![\[X_C=\frac{1}{C\omega}\qquad Z=\sqrt{\left(\frac{1}{C\omega}-L\omega\right)^2+R^2}\]](/images/math/6/c/3/6c3fbe0ba293a376c2459c429c798c64.png)
a kondenzátor, illetve a soros RLC-kör impedanciája.
A végeredmény jól ismert a váltóáramú áramkörök számításából.
Technikai alkalmazások
Atomi erő mikroszkópia
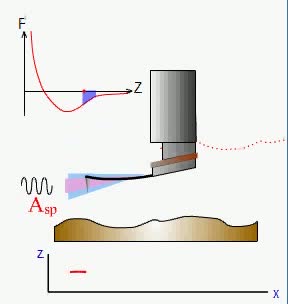
Az atomi erő mikroszkópia (AFM) tizednanométer felbontású vizsgálati módszer, amellyel felületeken, vagy akár egyes molekulákban lehet vizsgálni az atomok közti erőket.
A mikroszkóp érzékelője egy apró, rugalmas kar, a végén egy kis csúccsal, amely nanométeres távolságra van a vizsgált mintától. Az apró, rugalmas kar kis csillapítással rezeghet a mintára merőleges irányban. A gerjesztést a kar rögzített végénél egy piezo kristály biztosítja, amely úgy van hangolva, hogy frekvenciája a kar rezonanciafrekvenciája közelében (de kicsit fölötte) legyen. Ennek hatására a kar szabad vége a kis csúccsal néhány nanométeres amplitúdóval rezeg. A rezgés fázisát és amplitúdóját a kis karról visszaverődő lézersugárral lehet mérni. A csúcs (melynek görbületi sugara nanométer nagyságrendű) és a minta közt atomi léptékű erőhatások lépnek fel, melyek erősen függenek a távolságtól. Ha a kis csúcs és a minta távolsága változik, a rezgő rendszer sajátfrekvenciája kicsit eltolódik, és a rezgés gerjesztéshez viszonyított fázisa és amplitúdója – a rezonanciacsúcs közelében – meredeken változik. A fázis (vagy az amplitúdó) változását a lézersugár segítségével érzékelni lehet, és egy visszacsatoló elektronika segítségével a gerjesztés frekvenciáját úgy lehet változtatni, hogy a fázis (vagy az amplitúdó) állandó maradjon. Így néhány pN (10-12 N) nagyságú erők távolságfüggését lehet megmérni 0,1 nm-es (10-10 m-es) felbontással.
A minta piezo kristályokkal mozgatható, és így a minta felülete atomi méretskálán feltérképezhető.
Időmérés kvarc oszcillátorral
Legtöbb óra a mérendő időt egy rezgő rendszer periódusidejével hasonlítja össze: leszámolja, hány periódus játszódik le. Az ingaóra „időegysége” a fizikai inga lengésideje. Az ingaórában a gátszerkezet szabályozza a súlyok által meghajtott tengely mozgását: az inga minden lengésénél egy foggal engedi elfordulni. A mutatókat megfelelő áttétellel ez a tengely forgatja. Közben a gátszerkezeten keresztül pótlódik az inga energiavesztesége is: minden lengésnél egy kicsiny lökést kap az inga. A mechanikus karórákban a fizikai inga helyett rúgós torziós inga van, és az energiát súlyok helyett egy „felhúzott” spirálrúgó biztosítja, de a működési elv ugyanaz,mint az ingaórában. Az inga lengésidejét befolyásolja az alkatrészek hőtágulása és az óra mozgatása (pl. a tenger hullámzása, a kar mozgása miatt) – ezeket a hatásokat különböző mechanizmusokkal próbálták csökkenteni. A XVIII. században a tengeri hajózáshoz már olyan órákat tudtak készíteni, melyek 10 hét alatt legfeljebb 5 másodpercet siettek vagy késtek.
A mechanikus óráknál sokkal pontosabb (és olcsóbb) kvarcóra szintén egy rezgő rendszer sajátfrekvenciáját használja az időméréshez: ez a mechanikus órák ingáinál sokkal kisebb méretű és sokkal nagyobb frekvenciájú kvarc oszcillátor.
A rezgés frekvenciáját egy apró, hangvilla alakú kvarckristály sajátfrekvenciája határozza meg. A kvarckristály piezoelektromos anyag: elektromos erőtér hatására deformálódik, mechanikai deformáció hatására pedig elektromos feszültség keletkezik rajta. A kvarckristály két szemközti felületére vékony fémréteget gőzölnek. A kvarckristály rezgésekor ezen a kondenzátoron a mechanikai rezgés frekvenciájával megegyező frekvenciájú elektromos jel keletkezik. Ez a jel elektronikus erősítés után visszacsatolódik a kristályra, ez pótolja a mechanikai rezgés csekély energiaveszteségét.
A kvarc oszcillátor jósági tényezője nagyon nagy: akár 106 is lehet. Emiatt a kristály rezonanciagörbéje rendkívül éles. Bekapcsoláskor a gerjesztő zajból a kristály a sajátfrekvenciájának megfelelő frekvenciát erősíti fel, és azon fog rezegni.
A kvarckristály hőtágulása nagyon kicsi. Megfelelő irányú vágással a sajátfrekvencia hőmérsékletfüggése tovább csökkenthető. Nagypontosságú eszközökhöz a kristályt hőszabályzott tokba zárják.
A kvarcórákban a kristályt úgy vágják,hogy sajátfrekvenciája 32768 Hz = 215 Hz legyen. Ebből egy egyszerű digitális frekvenciafelező lánccal 1 Hz-es jelet lehet előállítani, ami vezérli az óra digitális vagy analóg kijelzőjét.
Különböző (néhány kHz-től néhány száz MHz-ig terjedő) frekvenciájú kvarc oszcillátorokat az órákon kívül sok más eszközben használnak: kvarc oszcillátorok adják a digitális integrált áramkörök órajelét, és stabilizálják például a rádióadók és vevők frekvenciáját is.
Nemlineáris rendszerek
A matematikai leírás nehézségei
A lineáris közelítés legtöbbször csak kis kitéréseknél jogos. Jó példa erre az ingamozgás. A fizikai inga mozgásegyenlete:![\[\Theta\ddot\varphi=-mgs\sin\varphi\]](/images/math/a/1/c/a1c545f0937907902d5983be83fa577d.png)
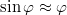 , és így a differenciálegyenlet
, és így a differenciálegyenlet ![\[\ddot\varphi+\omega_0^2\varphi=0\]](/images/math/3/9/f/39fccbc7458fa757c89bc2a057598afc.png)
![\[\omega_0^2=\frac{mgs}{\Theta}\]](/images/math/7/3/3/73355cc11187dc440c016ccb0d9fc8e5.png)
Ez a harmonikus rezgőmozgás jól ismert mozgásegyenlete.
Ha azonban a kitérés nem kicsi, akkor a közelítés nem alkalmazható, és a differenciálegyenlet nemlineáris lesz:![\[\ddot\varphi+k\sin\varphi=0\qquad{\rm ahol}\quad k=\sqrt{\frac{mgs}{\Theta}}\]](/images/math/2/f/e/2fe4c7f6d56addc0de3073155f464958.png)
![\[k=\sqrt{\frac{g}{l}}\]](/images/math/e/3/1/e3190b5a9edad1721b7f973b9435348a.png)
Ennek a differenciálegyenletnek sokkal bonyolultabb a megoldása: a rezgés nem lesz harmonikus, a periódusidő függ a rezgés amplitúdójától, és a kitérés időfüggvénye nem adható meg véges, elemi függvényekből álló kifejezéssel. A mozgás azonban így is periodikus, és az időfüggvények numerikus módszerekkel meghatározhatók.
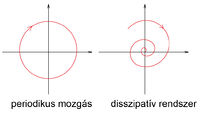
Az inga mozgása azonban az időfüggvényeknél jobban szemléltethető a fázistérben. A fázistér annyi dimenziós, ahány szabad paramétere (szabadsági foka) van a rendszernek. Az inga fázistere így kétdimenziós: szabad paraméter lehet például a szögkitérés és a szögsebesség. A csillapítatlan inga mozgását a fázistérben egy zárt görbe írja le (6/a ábra), a csillapított inga mozgása a stabil egyensúlyi állapothoz tartó spirál lesz (6/b ábra).
Két dimenzióban a görbék vagy önmagukba záródnak, vagy pedig egy egyensúlyi állapot (esetleg a végtelen) felé konvergálnak. Más lehetőség nincs: a görbék nem keresztezhetik saját magukat, hiszen egy adott állapotból (az instabil egyensúlyi állapotot kivéve) csak egyetlen – a mozgásegyenletek által egyértelműen meghatározott – irányba mozdulhat a rendszer.
Egészen más a helyzet, ha a rendszernek legalább három szabad paramétere van. A három- (vagy több-) dimenziós fázistérben már kialakulhatnak olyan görbék, amelyek nem konvergálnak se egy véges ponthoz, se a végtelenbe, de ugyanakkor soha nem záródnak önmagukba. Az ilyen rendszer kaotikusan viselkedhet.
A kaotikus viselkedés jellemzői és feltételei
A hétköznapi életben a kaotikus az össze-vissza, a teljesen kiszámíthatatlan szinonimája. Az nem meglepő, hogy nagyon összetett, nagyon sok szabad paraméterrel leírható rendszerek viselkedése bonyolult. Az 1970-es években azonban kiderült, hogy már néhány szabadsági fokú, egyszerű rendszerek is furcsán viselkedhetnek: annak ellenére, hogy az egyenletek determinisztikusak, a mozgás hosszútávon mégis megjósolhatatlan, és a kezdeti feltételek tetszőlegesen kicsi megváltoztatása esetén is a rendszer véges időn belül teljesen másképp fog viselkedni. Ez az ún. determinisztikus káosz (hiszen a kiszámíthatatlan viselkedést nem valamilyen véletlen hatás vagy zaj okozza). Ha a rendszert pontosan ugyanabból a kezdeti állapotból tudnánk újra elindítani, akkor a mozgása ugyanaz lenne. Azonban pontosan ugyanaz az állapot egy valóságos rendszernél nem valósítható meg, a legkisebb eltérés viszont már hosszútávon teljesen más mozgást eredményez (pillangóhatás).
A kaotikus viselkedést először egy nagyon-nagyon egyszerű, mindössze három szabad paramétert tartalmazó meteorológiai modellen figyelte meg Lorenz 1963-ban. Azóta nagyon sokféle kaotikus rendszert tanulmányoztak és írtak le, megszületett a káoszelmélet.
A kaotikus viselkedés szükséges feltétele, hogy a rendszernek legalább három szabad paramétere legyen, és a mozgásegyenletekben legyen nemlineáris tag. (Azonban egy ilyen rendszer sem biztos, hogy bármely kezdeti feltétel esetén kaotikusan viselkedik.)
Kaotikus kettős inga
A mozgás mérése V-scope-pal
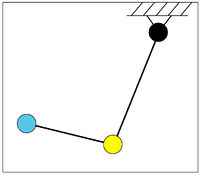
A kettős inga az egyik legegyszerűbb mechanikai rendszer, ami kaotikus viselkedést mutat. Kettős ingát úgy készíthetünk, hogy egy (matematikai vagy fizikai) inga végéhez csuklóval egy másik ingát erősítünk (7. ábra).
A kettős inga egy állapotát legegyszerűbben a két kar szöghelyzetével és szögsebességével adhatjuk meg – ez összesen négy paraméter. (Ha a csillapítás elhanyagolható, az energiamegmaradás miatt a négyből csak három paraméter változhat függetlenül.) A rendszer differenciálegyenleteiben megjelennek szinuszos, tehát nemlineáris tagok (a nehézségi erő forgatónyomatéka a szögkitérés szinuszával arányos), így a rendszer valóban kaotikusan viselkedhet.
A kaotikus kettős inga mozgásának kísérleti vizsgálatára többféle lehetőség van: a tengelyek szögelfordulását mérni lehet a csuklókba szerelt potenciométerek segítségével, vagy a mozgásról készült videofelvétel számítógépes elemzésével is. Itt a BME Fizika Tanszék fizikus hallgatói laboratóriumában lévő V-scope mérőrendszert, és az azzal készült mérések eredményét mutatjuk be. (Részletesen itt, BME-s domain-ről szabadon elérhető.)
A V-scope egy háromdimenziós ultrahangos nyomkövető rendszer. A rendszer részei a mozgó testre rögzíthető infravörös vevőt és ultrahang adót tartalmazó gombocskák, három infravörös adót és ultrahang vevőt tartalmazó rögzített helyzetű torony és egy mikroszámítógép. A tornyok kódolt infravörös jellel megszólítják valamelyik gombocskát, amely ultrahang jellel válaszol. A tornyok érzékelik az ultrahang jelet, és mérik az infravörös jel kibocsátása és az ultrahang jel beérkezése közt eltelt időt. Az időkésésből – a hőmérsékletfüggő hangsebesség ismeretében – kiszámítható a gombocska távolsága az egyes tornyoktól, majd a három távolságból – a tornyok helyzetének ismeretében – meghatározható a gombocska pillanatnyi helyzete – a mérés körülményeitől függően akár néhány mm pontossággal. Az eljárás folyamatos ismétlésével (akár másodpercenként százszor) a gombocska pályája nyomonkövethető. Az infravörös jelben lévő kódra egyszerre csak egy gombocska válaszol, így a felváltva küldött különböző kódokkal több gombocska (maximum három) mozgása is mérhető. A tornyok jeleit a mérés közben a mikroszámítógép dolgozza fel, és az egyes gombocskák koordinátáit az idő függvényében a számítógépnek továbbítja, ahol egy szoftverrel a mozgások megjeleníthetők, illetve az adatok más számításokhoz exportálhatók.
A kaotikus inga mérésekor az origót a nagy kar forgástengelyéhez állítjuk be, a két gombocskát pedig a karok végeire rögzítjük: a „sárga” gombocskát a nagy kar végére (a két kart összekapcsoló csuklóra), a „kék” gombocskát pedig a kis kar szabad végére. A „sárga” gombocska koordinátáiból a nagy kar szöghelyzete közvetlenül számítható, a két gombocska relatív helyzetéből pedig meghatározható a kis kar szöghelyzete is. (Itt külön számítási nehézséget jelent a körbefordulások figyelembevétele: elegendően nagy kezdeti energia esetén a kis kar többször is átfordulhat.)
A kaotikus viselkedés szemléltetése
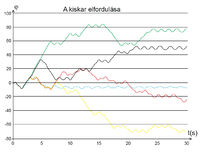
Ha az ingát a lehető legpontosabban ugyanabból a helyzetből többször is elindítjuk, akkor már az egyszerű megfigyelés alapján is láthatjuk, hogy az egyes mozgások jelentősen eltérnek egymástól. A mérési adatok alapján kiszámolhatjuk a karok szöghelyzetét az idő függvényében, és egy koordinátarendszerben ábrázoljuk az „azonos” helyről indított mozgások görbéit (8. ábra). Jól megfigyelhető, hogy a görbék néhány másodpercig vonalvastagságon belül megegyeznek, majd – a kezdeti állapotok közt szükségszerűen meglévő kicsiny eltérések miatt – szétválnak, és teljesen eltérően haladnak tovább. A súrlódás és légellenállás miatt az ingák lassan megállnak, de a végállapotok közt 10-20 fordulat (kb. 60-120 radián) különbség is lehet.
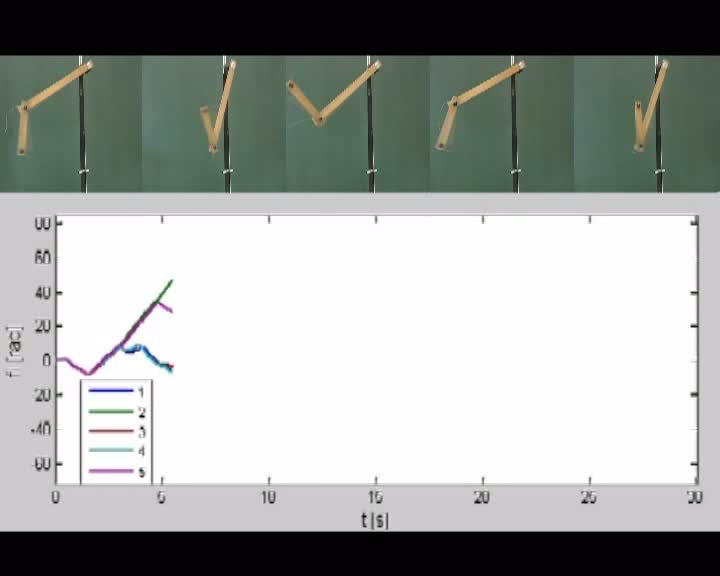
A filmen egyszerre láthatjuk négy „azonos” helyzetből elindított mozgásról készült videofelvételt és a mozgások V-scope-os mérése alapján készült, a kis kar szögelfordulását ábrázoló grafikont. Megfigyelhető, hogy a görbék ott válnak hirtelen szét, ahol a kis kar instabil egyensúlyi helyzet közelébe kerül.
Szimulációk
A kettős inga mozgásegyenlete a Lagrange-függvénye alapján felírható, és adott kezdőfeltétel esetén numerikus módszerekkel megoldható. A megoldás ábrázolható animációval, időfüggvényekkel vagy a fázistérben. Az interneten rengeteg ilyen szimuláció található. Egy példa.
A numerikus megoldást ugyanazzal a kezdőfeltétellel megismételve tökéletesen reprodukálódik (a szimulációban a kezdeti állapot lehet pontosan ugyanaz – szemben a valóságos kísérlettel). A kaotikus viselkedés szemléltetéséhez a kezdeti feltételekbe mesterségesen kell bevinni a kicsiny eltérést. Egy példa letölthető programmal.
Mechanikai hullámok
A hullámok jellemző adatai
A hullám a természet alapvető mozgásformája. Itt most elsősorban mechanikai hullámok tulajdonságaival foglalkozunk, de a megállapítások többsége más hullámokra (elektromágneses hullámok, kvantummechanikai hullámok) is igazak.
A mechanikai hullám egy rugalmas közegben tovaterjedő „zavar”. Hirtelen, rövid zavarok keltette hullám a lökéshullám. Periodikus zavar hatására térben és időben periodikus „mintázat” alakul ki. Gyakorlati és elméleti szempontból is kiemelkedően fontosak a harmonikus hullámok, ahol a közeg pontjainak kitérése térben és időben is szinuszosan változik. Harmonikus hullámok szuperpozíciójaként bármely más hullám leírható (periodikus hullámok Fourier-sor, aperiodikus hullámok Fourier-integrál segítségével).
Megkülönböztetünk haladó és állóhullámokat. A haladó hullámban a hullám valamely fázisa (pl. a „hullámhegy” vagy a „hullámvölgy”) egyenletes sebességgel mozog. A sebesség függ a közeg, és sok esetben a hullám tulajdonságaitól is. Haladó hullámok interferenciája állóhullámokat eredményezhet: a közeg egyes pontjai nyugalomban vannak (csomópontok, csomóvonalak vagy csomófelületek), míg más pontjai maximális amplitúdóval rezegnek (duzzadóhelyek).Különböző közegekben kialakuló állóhullámok láthatók a következő videókon:
A mechanikai hullámok terjedhetnek egy- két- vagy háromdimenziós közegben. Egydimenziósak például a húrokon, pálcákon vagy légoszlopokon kialakuló hullámok, tipikus kétdimenziós hullámok a vízfelületeken kialakuló felületi hullámok, a hang pedig háromdimenziós hullám. Homogén, izotróp közegben egy pontszerű forrásból kiinduló hullámban az azonos fázisú pontok (hullámfrontok) gömbfelületen helyezkednek el (gömbhullám). A forrástól nagy távolságra a hullámfront már közelítőleg sík: a síkhullámokban a hullámterjedés egy kitüntetett irányban történik, így ezek az egydimenziós hullámokhoz hasonlóan leírhatók.
A közeg pontjainak kitérése lehet párhuzamos a hullám terjedési irányával, vagy merőleges arra. Az elsőt longitudinális hullámnak nevezzük, ilyen például a hang terjedése gázokban és folyadékokban. Ha a közeg pontjai a terjedési irányra merőleges rezgést végeznek, akkor a hullám transzverzális. Ilyen hullámok alakulhatnak ki például megfeszített húrokon. A transzverzális hullámoknál a közeg pontjai a terjedés irányára merőleges bármely irányban rezeghetnek. Ha a rezgés csak egy kitüntetett irányban történik, akkor a hullám polarizált. Ezzel a jelenséggel részletesebben az optika foglalkozik: a fény is transzverzális (elektromágneses) hullám.
A harmonikus haladó hullám jellemző adatai:
Az  amplitúdó – a rezgésekhez hasonlóan – a közeg pontjainak maximális kitérése.
amplitúdó – a rezgésekhez hasonlóan – a közeg pontjainak maximális kitérése.
 periódusidővel, az
periódusidővel, az  frekvenciával, vagy az
frekvenciával, vagy az  körfrekvenciával.
körfrekvenciával. ![\[f=\frac{1}{T}\qquad\omega=2\pi f=\frac{2\pi}{T}\]](/images/math/b/0/1/b01b50c9ccbc422114bd8e10b6d9e11d.png)
 hullámhosszal jellemezhetjük: ez két, egymáshoz legközelebb lévő, azonos fázisú pont távolsága. Használatos a
hullámhosszal jellemezhetjük: ez két, egymáshoz legközelebb lévő, azonos fázisú pont távolsága. Használatos a  hullámszám is:
hullámszám is: ![\[k=\frac{2\pi}{\lambda}\]](/images/math/2/4/2/24240ca20d73d4676ff76f4f24fe1541.png)
![\[\Psi(t,x)=A\sin(\omega t-kx+\varphi)\]](/images/math/8/2/e/82e0f0d263103c8c692f27c97b5cd4c4.png)
 a kezdőfázis. A hullám fázisát a szinusz függvény argumentumában lévő kifejezés adja meg. A fázis állandó, ha
a kezdőfázis. A hullám fázisát a szinusz függvény argumentumában lévő kifejezés adja meg. A fázis állandó, ha ![\[\omega t-kx={\rm const.}\]](/images/math/7/c/5/7c57d65781188d56ba93cfac90c1e69c.png)
![\[x=\frac{\omega}{k}t+{\rm const.}\]](/images/math/2/4/d/24dccae2d7473b7f3e3eee9e67a2a0eb.png)
![\[c=\frac{\omega}{k}=f\lambda\]](/images/math/2/f/8/2f8cffeaa756cf1f5f1bdce4d844d889.png)
A hullám  terjedési sebessége nem a közeg egyes pontjainak sebességét jelenti, hanem egy adott fázisú állapot haladási sebességét. (Ezért szokás ezt a sebességet fázissebességnek nevezni. Olyan hullámoknál, ahol a fázissebesség függ a hullám frekvenciájától is – ez a diszperzió jelensége – a nemharmonikus hullámok harmonikus összetevői más-más sebességgel haladnak, így a hullámforma időben változhat, és egy „hullámcsomag” a fázissebességtől különböző csoportsebességgel halad.)
terjedési sebessége nem a közeg egyes pontjainak sebességét jelenti, hanem egy adott fázisú állapot haladási sebességét. (Ezért szokás ezt a sebességet fázissebességnek nevezni. Olyan hullámoknál, ahol a fázissebesség függ a hullám frekvenciájától is – ez a diszperzió jelensége – a nemharmonikus hullámok harmonikus összetevői más-más sebességgel haladnak, így a hullámforma időben változhat, és egy „hullámcsomag” a fázissebességtől különböző csoportsebességgel halad.)
Hangok esetében a hang erősségét a hullám amplitúdója (illetve az amplitúdó négyzetével arányos intenzitás), a hang magasságát pedig a hullám frekvenciája határozza meg. Mindkét skála logaritmikus: Az észlelt hangerősség az intenzitás logaritmusával arányos (decibel skála). A zenei hangközök pedig nem a frekvenciák különbségétől, hanem a frekvenciák arányától függenek. A zenei hangok nem szinuszos hullámok: az alapfrekvencia mellett megjelennek annak többszörösei is. A hangszínt ezeknek a felharmonikusoknak a relatív erőssége határozza meg.
A hullámok terjedését különböző peremfeltételek esetén a hullámfüggvény segítségével meg lehet határozni. A jellegzetes hullámjelenségeket több modell alapján is értelmezni lehet, ilyen például a Huygens-Fresnel-elv. Itt most csak a jelenségek tapasztalati leírást adjuk, levezetés nélkül.
Visszaverődés és törés
A tapasztalat szerint, ha egy hullám két különböző tulajdonságú közeg határához érkezik, akkor – részlegesen vagy teljesen – visszaverődik, az új közegben pedig az eredeti iránytól eltérő irányban terjed tovább. Ez a visszaverődés és a törés jelensége.
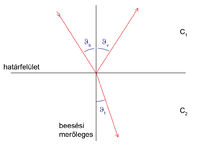
A beérkező hullám terjedési iránya (hullámszámvektora) és a határfelület normálisa közti szög az 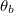 beesési szög, a visszavert és a megtört hullám terjedési iránya és a határfelület normálisa közti szögek pedig az
beesési szög, a visszavert és a megtört hullám terjedési iránya és a határfelület normálisa közti szögek pedig az 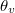 visszaverődési szög, illetve az
visszaverődési szög, illetve az 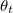 törési szög. Mind a négy egyenes egy síkban fekszik.
törési szög. Mind a négy egyenes egy síkban fekszik.
![\[\theta_b=\theta_v\]](/images/math/1/3/9/139af28deadfdf0ba0ba503ade309d54.png)
azaz a beesési és a visszaverődési szög megegyezik.
A törés törvényét a Snellius-Descartes-törvény adja meg:![\[\frac{\sin\theta_b}{\sin\theta_t}=\frac{c_1}{c_2}\]](/images/math/4/1/2/4125a8d86f597d78133e296586dfb8e6.png)
ahol 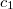 és
és 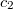 a hullám terjedési sebessége az első és a második közegben. (A terjedési sebességek hányadosát – elsősorban az optikában – szokás a két közeg relatív törésmutatójának nevezni. Ha a sebesség függ a frekvenciától, akkor a törésmutató is frekvenciafüggő.) Ha
a hullám terjedési sebessége az első és a második közegben. (A terjedési sebességek hányadosát – elsősorban az optikában – szokás a két közeg relatív törésmutatójának nevezni. Ha a sebesség függ a frekvenciától, akkor a törésmutató is frekvenciafüggő.) Ha 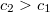 , akkor nagy beesési szögek esetén a képlet nem ad eredményt
, akkor nagy beesési szögek esetén a képlet nem ad eredményt 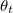 -re. Ilyenkor a hullám valóban nem lép be a második közegbe (teljes visszaverődés).
-re. Ilyenkor a hullám valóban nem lép be a második közegbe (teljes visszaverődés).
A videó egy egydimenziós hullám visszaverődését szemlélteti MATLAB szimuláció segítségével. A szimuláció forráskódja, illetve további részletek a Matlab szimulációk oldalon találhatók.
Elhajlás és interferencia
Ha a hullám egy nyíláson vagy egy akadály mellett halad el, akkor a tapasztalat szerint az akadály mögött behatol az árnyéktérbe is. Ez az elhajlás, vagy diffrakció jelensége. Az elhajlás akkor számottevő, ha az akadály mérete összemérhető a hullámhosszal (vagy kisebb annál).
Az elhajló hullámok az akadály mögött szuperponálódnak egymással. A hullámok összeadódása az interferencia jelensége. Két azonos frekvenciájú hullám a hullámok közötti fáziskülönbségtől függően erősíthetik, vagy gyengíthetik (esetleg kiolthatják) egymást. Gyorsan változó fáziskülönbség esetén az interferencia nem figyelhető meg (hiszen az erősítések és gyengítése kiátlagolódnak), azonban ha a fáziskülönbség időben állandó, akkor a hullámtér bizonyos helyein a hullámok erősítik, más helyeken viszont kioltják vagy gyengítik egymást.
Az interferencia alapvető hullámjelenség, mindenhol előfordul, ahol több hullám szuperponálódik. Nem csak az elhajlással együtt figyelhető meg, hanem például (többszörös) visszaverődés esetén is.
Kis mértékben eltérő frekvenciájú hullámok összeadódásakor a fáziskülönbség – és ezzel együtt az erősítés és a kioltás – időben lassan változik. Ez a lebegés jelensége, amit például hangszerek hangolására lehet felhasználni. (Ha a két frekvencia megegyezik, a lebegés megszűnik.)
A fenti jelenségek jól megfigyelhetők a hullámkádról készült kísérleti videókon (1-5. videó: hullámkeltés; 6-8. videó: hullámok visszaverődése; 9-11. videó: hullámok elhajlása; 12-14. videó: hullámok törése):
| 1. Teljes méret |
2. Teljes méret |
3. Teljes méret |
4. Teljes méret |
5. Teljes méret |
6. Teljes méret |
7. Teljes méret |
| 8. Teljes méret |
9. Teljes méret |
10. Teljes méret |
11. Teljes méret |
12. Teljes méret |
13. Teljes méret |
14. Teljes méret |
Doppler-effektus
Közismert tapasztalat, hogy a mozgó vonat sípjának, vagy a mentőautó szirénájának a hangját másképp halljuk, amikor a jármű közeledik, vagy amikor távolodik. Ez a jelenség a Doppler-effektus: ha a hullám forrása vagy a megfigyelő mozog, akkor a megfigyelő a hullám frekvenciáját a hullámforrás valódi frekvenciájától eltérőnek fogja érzékelni.
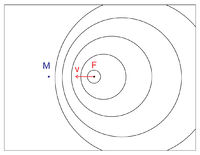
Az ábra alapján is látszik, hogy ha a hullámforrás közeledik a nyugalomban lévő megfigyelőhöz, akkor az észlelt frekvencia a hullámforrás frekvenciájánál nagyobb lesz (hanghullámok esetében magasabb hangot hallunk), míg távolodó forrás esetén az észlelt frekvencia csökken (mélyebb hang).
Ha a forrás és a megfigyelő is mozog, akkor az észlelt frekvencia:![\[f=\frac{c+v_m}{c-v_f}f_0\]](/images/math/3/2/7/3270916fa47c41981cc4b69accca00e8.png)
ahol  a hullám terjedési sebessége a közegben,
a hullám terjedési sebessége a közegben, 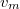 és
és 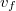 a megfigyelő és a forrás sebessége a közeghez képest (mindkettő akkor pozitív, ha egymás felé mozognak), és
a megfigyelő és a forrás sebessége a közeghez képest (mindkettő akkor pozitív, ha egymás felé mozognak), és  a forrás frekvenciája.
a forrás frekvenciája.
 relatív sebessége szerepel:
relatív sebessége szerepel: ![\[f=\sqrt{\frac{c+v}{c-v}}f_0\]](/images/math/b/f/1/bf1ec6d2c78a23e321ccb457a2b2cd3d.png)
( most is akkor pozitív, ha a forrás és a megfigyelő közelednek egymáshoz.)
most is akkor pozitív, ha a forrás és a megfigyelő közelednek egymáshoz.)
Ultrahangos orvosi diagnosztika
Piezo hangforrás és érzékelő
Az emberi fül a 20 Hz és 20 kHz közötti frekvenciájú hangokat hallja. Az ennél nagyobb frekvenciájú mechanikai hullámokat ultrahangnak nevezzük. Az állatok egy része érzékeli az ultrahangokat: a denevérek és bizonyos cetfélék az általuk kibocsátott és a tárgyakról visszavert ultrahang segítségével tájékozódnak. Számos ipari és hétköznapi alkalmazása is van az ultrahangnak: például felületek tisztítása, üreges testek roncsolásmentes vizsgálata, távolságmérés vagy vízporlasztás a páratartalom növeléséhez.
Az egyik kiemelkedő alkalmazás, amivel részletesebben foglalkozunk az ultrahangos orvosi diagnosztika. Ezzel a képalkotó eljárással az emberi testben részben elnyelődő, részben visszaverődő ultrahang segítségével a szervezet belsejében lévő szövetekről, a szív működéséről, illetve a magzatról és a magzat szerveiről nyerhető információ – alapvetően káros mellékhatások nélkül.
Diagnosztikai célokra 2-18 MHz-es ultrahangot használnak. A nagyobb frekvencia (kisebb hullámhossz) előnye a jobb térbeli felbontás, a kisebbé a nagyobb behatolási mélység. (Az ultrahang a testben kb. 1500 m/s sebességgel halad, így ehhez a frekvenciatartományhoz kb. 1-0,1 mm-es hullámhossz tartozik. A képalkotással a hullámhossznál kisebb részletek nem különböztethetők meg.)
Az ultrahangok keltésére és érzékelésére is piezo kristályokat használnak (általában ugyanaz a kristály egyben hangforrás és érzékelő is). Az eszközt a bőrre helyezik, amit a vizsgálathoz a jobb hangvezetés érdekében egy vízalapú géllel kennek be. A kibocsátott ultrahang impulzusok különböző helyekről (elsősorban szövethatárokról) visszaverődnek, a visszaverődött jelet az eszköz érzékeli (elektromos jellé alakítja), és jelfeldolgozásra a számítógépnek továbbítja.
A szkennelés (pásztázás) elve és megvalósítása
Az ultrahangforrás egyszerre csak egy irányba bocsát ki jelet, és csak ebből az irányból érkezik válaszjel is. A kép úgy alakul ki, hogy az ultrahangnyaláb végigpásztázza a vizsgálandó területet. A pásztázás (szkennelés) elve jól ismert a katódsugárcsöves televíziókból és monitorokból: ott az elektronsugár pásztázza soronként végig a képernyőt, és így alakul ki a kép.
A korai ultrahangos készülékekben a nyaláb mozgatását az ultrahang kibocsátó kristály forgatásával oldották meg. A modern készülékekben a pásztázást a hullámok interferenciája segítségével valósítják meg: Egyetlen piezo kristály helyett sok apró kristályból áll a forrás, a hullámfront az elemi források hullámainak szuperpozíciójaként, azaz a hullámok interferenciájával jön létre. Ha az elemi hullámforrásokból azonos fázisban indul a hang, a kialakuló hullámfrontok a felülettel párhuzamosak lesznek, és így a hullám erre merőlegesen halad. Ha azonban a szomszédos elemi hullámforrásokból egy kicsiny fáziskülönbséggel indulnak a hullámok, akkor a kialakuló hullámfront (és így a nyaláb iránya) már más lesz (11. ábra). Ezzel a módszerrel sokkal egyszerűbben és gyorsabban (mozgó alkatrészek helyett elektronikával) lehet a nyaláb irányát változtatni.
Mélységi információ, 3D megjelenítés
A mélységi információt, azt hogy honnan verődik vissza a hang, elsősorban a visszaérkező impulzus késéséből lehet meghatározni. A testet felépítő szövetek többsége nagy víztartalmú, és így a hang terjedési sebessége csak kicsit változik, lényegében megegyezik a sós vízben mért hangsebességgel. Ez alapján az időkésésből a mélység számolható.
Ezen kívül a jobb felbontás érdekében a kibocsátott ultrahang nyalábot a vizsgálandó mélységnek megfelelően fókuszálják. A nyaláb fókuszálására lencséket is lehet használni, de kényelmesebben megvalósítható – a pásztázáshoz hasonlóan – az elemi hullámforrások fáziskülönbségével. Így a fókusztávolság folyamatosan változtatható, különböző mélységből nyerhető éles kép.
A pásztázás és a mélységi információ alapján a test belsejében lévő szövethatárok és egyéb objektumok helye három dimenzióban meghatározható. Ebből az adatbázisból a számítógép segítségével már 3D képeket lehet készíteni. A magzatokról készült ultrahangos képek jól ismertek. Ugyanakkor a képek értelmezéséhez, az egyes elváltozások vagy szövetsérülések (pl. egy izomszakadás, bevérzés) felismeréséhez a technikán kívül a szakorvosi tapasztalatra is feltétlenül szükség van.
A vér áramlási sebességének mérése Doppler-eltolódás alapján
Ha egy hullám mozgó felületről verődik vissza, akkor a visszavert hullámnak megváltozik a frekvenciája. A jelenség a Doppler-effektus egy speciális esete, amely az egymáshoz képest mozgó forrás és megfigyelő esetéhez hasonlóan leírható. A frekvenciaeltolódásból meghatározható a visszaverő felület sebessége (pontosabban a sebesség felületre merőleges komponense).
Ezen az elven működik a Doppler-echokardiográfia, amellyel a szívben (vagy az erekben) áramló vér sebessége meghatározható. Az ultrahang visszaverődik a vér alakos összetevőiről (például a vörösvérsejtekről), és frekvenciája a vér sebességétől függő mértékben megváltozik. Ezt az információt az amúgy fekete-fehér ultrahangos képen színezéssel jelölik, így a kép színei alapján látható, hogy hol nagyon gyors (örvénylés, a szívbillentyű tökéletlen zárása miatti visszaáramlás), illetve hol nagyon lassú (pl. elzáródás) a vér áramlása.
Vissza a Kísérleti fizika 1. nyitóoldalára
3. Megmaradási törvények a mechanikában
4. Rezgések