Magnetosztatika példák - Kör alakú áramhurok mágneseses momentuma

Feladat

1. Határozzuk meg a mágneses dipólusmomentumát egy kör alakú áramhuroknak, ha a sugara $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ és a középpontjában a mágneses indukció nagysága $\setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0%$!

Megoldás

Induljunk ki a mágneses momentum definíciójából:

$\[\vec{M}=I\vec{A}\]$

A gyűrű területét könnyen kiszámíthatjuk:

$\[A=R^2 \pi\]$

A gyűrűben folyó $\setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0%$ áramot pedig meghatározhatjuk a mágneses tér ismeretében. A Gyűrű alakú vezető mágneses tere feladatából tudjuk, hogy az $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú, $\setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0%$ árammal átjárt körív, mely $\setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0%$ középponti szög alatt látszódik, középpontjában síkjára merőleges mágneses teret indukál, melynek nagysága:

$\[B=\dfrac{\mu_0 I}{4 \pi R}\alpha\]$

A mi esetünkben egy teljes körvezető terét vizsgáljuk, tehát 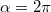$\setbox0\hbox{$\alpha=2\pi$}% \message{//depth:\the\dp0//}% \box0%$. Az $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú körvezető mágneses tere és a benne folyó áram között az összefüggés:

$\[B=\dfrac{\mu_0 I}{4 \pi R}2\pi=\dfrac{\mu_0 I}{2 R}\]$

Ebből kifejezve az áramot:

$\[I=\dfrac{2BR}{\mu_0}\]$

Tehát az $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú körvezető mágneses momentuma, melynek középpontjában $\setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0%$ a mágneses indukció nagysága:

$\[M=IA=\dfrac{2BR}{\mu_0}R^2 \pi=\dfrac{2\pi BR^3}{\mu_0}\]$