Magnetosztatika példák - Szolenoid mágneses tere (Ampere-féle gerjesztés)
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Beleznai (vitalap | szerkesztései) 2013. szeptember 30., 15:30-kor történt szerkesztése után volt.
Feladat
- Határozzuk meg a mágneses indukció nagyságát egy
 hosszúságú,
hosszúságú,  menetű szolenoidban, amelyben
menetű szolenoidban, amelyben  áram folyik gerjesztési törvény segítségével.
áram folyik gerjesztési törvény segítségével.
Megoldás
a.) Vegyünk fel egy 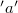
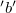
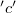
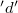 oldalakkal határolt téglalap alakú zárt hurkot, melynek
oldalakkal határolt téglalap alakú zárt hurkot, melynek 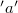 oldala
oldala  hosszúságú, és egybe esik a szolenoid tengelyével. Az erre merőleges
hosszúságú, és egybe esik a szolenoid tengelyével. Az erre merőleges 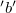 és
és 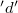 oldalai igen hosszúak, így a téglalap szintén
oldalai igen hosszúak, így a téglalap szintén  hosszúságú
hosszúságú 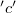 oldala olyan távol van a szolenoidtól, hogy annak tere ott már elhanyagolható.
Írjuk fel erre a zárt görbére az Amper-féle gerjesztési törvényt:
oldala olyan távol van a szolenoidtól, hogy annak tere ott már elhanyagolható.
Írjuk fel erre a zárt görbére az Amper-féle gerjesztési törvényt:
![\[\sum I=\oint \vec{H}\vec{dl}\]](/images/math/6/a/a/6aaa8b49e2de5a331efe6620c4dfcc74.png)
A zárt görbe által határolt területen átfolyik a szolenoid  darab menetének
darab menetének  árama, így a gerjesztési törvény:
árama, így a gerjesztési törvény:
![\[NI=\int_a \vec{H}\vec{dl}+\int_b \vec{H}\vec{dl}+\int_c \vec{H}\vec{dl}+\int_d \vec{H}\vec{dl}\]](/images/math/4/a/e/4ae37ef2c2ce3bbc77129fcd75373b2b.png)
A tekercs belsejére számított vonalintegrálja mellett a másik három integrál elhanyagolható.
Így kapott egyenlet:
![\[NI=Hl\]](/images/math/4/3/f/43f3d606ba460d88eac0b42383c61106.png)
Ebből kiszámolható az  árammal átjárt
árammal átjárt  hosszúságú szolenoid belsejében mérhető mágneses indukció:
hosszúságú szolenoid belsejében mérhető mágneses indukció:
![\[B=\dfrac{\mu_0 NI}{l}\]](/images/math/2/0/7/207641385b12448b0305980157b8c127.png)