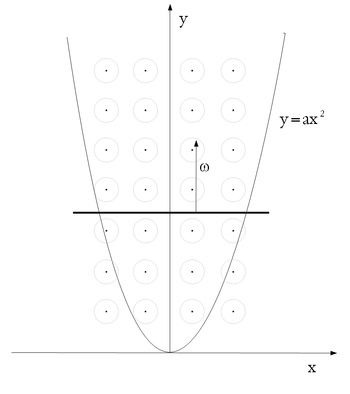
Magnetosztatika példák - Parabola alakú vezetőben kialakult indukált feszültség

Feladat

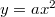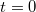1. Egy $\setbox0\hbox{$y = ax^2$}% \message{//depth:\the\dp0//}% \box0%$ egyenletnek megfelelően parabola alakúra hajlított vezetőt az xy síkra merőleges $\setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0%$ mágneses indukciójú térbe helyezzük. A $\setbox0\hbox{$t = 0$}% \message{//depth:\the\dp0//}% \box0%$ pillanatban az x tengellyel párhuzamos vezető 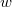$\setbox0\hbox{$w$}% \message{//depth:\the\dp0//}% \box0%$ gyorsulással elindul az 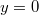$\setbox0\hbox{$y = 0$}% \message{//depth:\the\dp0//}% \box0%$ helyzetből a pozitív $\setbox0\hbox{$y$}% \message{//depth:\the\dp0//}% \box0%$ irányban. Állapítsuk meg az indukált feszültséget y függvényeként.
   

Megoldás

Először a vezetékek által bezárt görbe területét kell kiszámoljuk az $\setbox0\hbox{$y$}% \message{//depth:\the\dp0//}% \box0%$ és az idő függvényében.

A parabola alatti területet a következőképpen írhatjuk fel, amikor a rúd $\setbox0\hbox{$y$}% \message{//depth:\the\dp0//}% \box0%$ magasságában jár:

$\[\tilde{A} = 2\int_{0}^{\sqrt{\frac{y}{a}}} ax^2dx = \frac{2a^{-\frac{1}{2}}y^{\frac{3}{2}}}{3}\]$

A a görbe alatti terület ismeretében kiszámítható a vezető által körbezárt terület is:

$\[A = 2\cdot(y\cdot\sqrt{\frac{{y}}{a}}-\tilde{A}) = \frac{4}{3} a^{-\frac{1}{2}}\cdot y^{\frac{3}{2}} \]$

Az indukált feszültség a Faraday féle indukciós törvény alapján:

$\[U = -B\cdot\frac{\partial A}{\partial t} = -B\cdot\frac{\partial A}{\partial y}\cdot \frac{\partial y}{\partial t}\]$

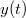Az $\setbox0\hbox{$y(t)$}% \message{//depth:\the\dp0//}% \box0%$ függvény kiszámolható a kinematikai egyenletekből:

$\[y(t) =\frac{1}{2}wt^2 \]$

Amiből az indukált feszültség az $\setbox0\hbox{$y$}% \message{//depth:\the\dp0//}% \box0%$ függvényében:

$\[U = -B\cdot\sqrt{\frac{2w}{a}}\cdot y \]$