Munka, energia - 2.4.6
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. október 15., 10:00-kor történt szerkesztése után volt.
Feladat
- (2.4.6) Egy
 tömegű,
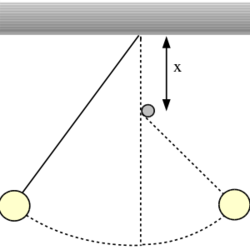
tömegű,  hosszúságú matematikai ingát vízszintes helyzetéből elengedünk. Függőleges helyzetében a kötél egy csapocskán megakad, így az inga az ábrán látható módon lendül tovább.
hosszúságú matematikai ingát vízszintes helyzetéből elengedünk. Függőleges helyzetében a kötél egy csapocskán megakad, így az inga az ábrán látható módon lendül tovább.
- a) Mi a dinamikai feltétele annak, hogy az inga további mozgása során le tudjon írni egy teljes kört?
- b) Hova kell ehhez helyezni a csapocskát?
- c) Hogyan alakul a test pályája ellenkező esetben? (szöveges válasz)
- d) Hova kell helyezni a csapocskát, hogy a c) esetben ismét az indítás magasságába jusson fel?
Megoldás
- a) A kérdésre naivan azt válaszolhatnánk, hogy
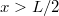 , mert ekkor a körpálya legfelső pontja lejjebb lenne, mint a kezdeti állapot, tehát lenne elegendő energiája a testnek "felmászni" a körpálya legfelső pontjáig. A gondolatmenet azonban hibás, mert ha a test sebessége nagyon kicsi a körpálya legfelső pontja környékén, akkor a testre ható gravitációs erő hatására az letér a körpályáról és lényegében ferde hajítás szerint mozogna. Tegyük fel, hogy a test sebessége
, mert ekkor a körpálya legfelső pontja lejjebb lenne, mint a kezdeti állapot, tehát lenne elegendő energiája a testnek "felmászni" a körpálya legfelső pontjáig. A gondolatmenet azonban hibás, mert ha a test sebessége nagyon kicsi a körpálya legfelső pontja környékén, akkor a testre ható gravitációs erő hatására az letér a körpályáról és lényegében ferde hajítás szerint mozogna. Tegyük fel, hogy a test sebessége 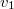 a körpálya legmagasabb pontján. A körpálya sugara
a körpálya legmagasabb pontján. A körpálya sugara 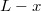 . A testre ható erők a gravitációs erő és a kötélerő. A kötélerő azonban nem lehet negatív, így
. A testre ható erők a gravitációs erő és a kötélerő. A kötélerő azonban nem lehet negatív, így![\[F_{g}+K=m\frac{v_{1}^{2}}{L-x}\]](/images/math/b/d/5/bd52393fb4773dc0874c4444ad8c693d.png) a dinamikai feltétele annak, hogy a test egy teljes körpályát írjon le.
a dinamikai feltétele annak, hogy a test egy teljes körpályát írjon le.![\[0<\frac{v_{1}^{2}}{L-x}-g\]](/images/math/b/e/e/bee27b6937006c4a4891e545071800f6.png)
- b) A
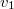 sebesség energetikai megfontolásokkal határozható meg. A kezdeti állapot és a körpálya legmagasabb pontjának szintkülönbsége
sebesség energetikai megfontolásokkal határozható meg. A kezdeti állapot és a körpálya legmagasabb pontjának szintkülönbsége 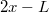 , így Ezzel behelyettesítve a dinamikai feltételbe
, így Ezzel behelyettesítve a dinamikai feltételbe![\[\frac{1}{2}mv_{1}^{2}=mg(2x-L)\qquad\Rightarrow\qquad v_{1}^{2}=2g(2x-L)\,.\]](/images/math/b/3/d/b3d404558fa198039b01635b80bce850.png) adódik. Tehát legalább
adódik. Tehát legalább![\[x>\frac{3L}{5}\]](/images/math/2/8/2/282e6be4330c012f0effb2538e04d3c0.png)
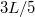 távolságban kell a csapocskát elhelyezni ahhoz, hogy egy teljes kört leírjon a test.
távolságban kell a csapocskát elhelyezni ahhoz, hogy egy teljes kört leírjon a test.
- c) Ha ennél kisebb az
 távolság, akkor a továbblendülés után az inga egy ideig körpályán haladna, de a pályáról le fog térni egy ponton a gravitációs erő hatására és ferde hajító mozgással mozog tovább.
távolság, akkor a továbblendülés után az inga egy ideig körpályán haladna, de a pályáról le fog térni egy ponton a gravitációs erő hatására és ferde hajító mozgással mozog tovább.
- d) Ha
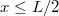 , akkor nincs fizikai korlátja annak, hogy a test visszajusson az eredeti magasságig. Azonban a ferde hajítású mozgás legfelső pontján a testnek lesz egy vízszintes irányú sebessége, és egyúttal mozgási energiája. Ez azt jelenti, hogy a kezdeti energia nem elegendő ahhoz, hogy a test az eredeti magasságig jusson. Egyedül az
, akkor nincs fizikai korlátja annak, hogy a test visszajusson az eredeti magasságig. Azonban a ferde hajítású mozgás legfelső pontján a testnek lesz egy vízszintes irányú sebessége, és egyúttal mozgási energiája. Ez azt jelenti, hogy a kezdeti energia nem elegendő ahhoz, hogy a test az eredeti magasságig jusson. Egyedül az 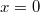 esetben lehetséges mégis, amikor a test egyszerűen csal átlendül a másik oldalra.
esetben lehetséges mégis, amikor a test egyszerűen csal átlendül a másik oldalra.
- a) A kérdésre naivan azt válaszolhatnánk, hogy