Munka, energia - 2.3.6
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Werner (vitalap | szerkesztései) 2014. október 14., 18:15-kor történt szerkesztése után volt.
Feladat
- (*2.3.6 alapján)
- a.) Első kozmikus sebességnek nevezzük azt a sebességet, amennyivel a Föld felszínén vízszintesen el kell lőni egy testet, hogy körpályán megkerülje a Földet, feltéve hogy nincs légellenállás. Mekkora az első kozmikus sebesség a Földön?
- b.) Második kozmikus sebességnek nevezzük azt a sebességet, amennyivel elindítva egy testet a Föld felszínéről, el tud szabadulni a Földtől. Mekkora a második kozmikus sebesség?
- (Adatok:
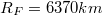 ,
, 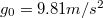 )
)
Megoldás
- a.) A felszínen a gravitációs gyorsulás
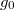 , ha éppen körbe repüli a Földet, úgy a centripetális gyorsulást az
, ha éppen körbe repüli a Földet, úgy a centripetális gyorsulást az 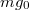 erő hozza létre: ebből
erő hozza létre: ebből![\[m g_0 = m \frac{v_1^2}{R} \, ,\]](/images/math/8/c/f/8cfa770e6e626ea6ddf6fd6367f09f72.png)
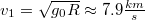 .
.
- b.) Bár nem szükséges a feladat megoldásához, de didaktikai okokból vezessük le a centrális gravitációs térerősség helyzeti energiáját! A gravitációs erő kifejezése a Föld középpontjától
 távolságban ahol
távolságban ahol![\[F = - \gamma \frac{m M}{r^2} \, ,\]](/images/math/e/a/7/ea70c7c530c403ee8fb72ffc08d10ddd.png)
 a Föld tömege,
a Föld tömege,  a gravitációs állandó. Bár ezeket megadhatnánk, de a kozmikus sebesség számításához elegendő lesz
a gravitációs állandó. Bár ezeket megadhatnánk, de a kozmikus sebesség számításához elegendő lesz 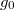 és
és  ismerete. A negatív előjellel jelezzük, hogy az erő befelé, a Föld középpontja felé mutat.
ismerete. A negatív előjellel jelezzük, hogy az erő befelé, a Föld középpontja felé mutat.
- A gravitációs helyzeti energia felírásához meg kell adnunk egy
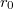 távolságot, ahol felvesszük a helyzeti energia nulla szintjét. A Föld középpontjától
távolságot, ahol felvesszük a helyzeti energia nulla szintjét. A Föld középpontjától  távolságra a helyzeti energia ezután megadható, ha kiszámítjuk a gravitációs erő munkáját, amíg
távolságra a helyzeti energia ezután megadható, ha kiszámítjuk a gravitációs erő munkáját, amíg  -ből
-ből 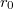 -ba visszük a tömegpontot. Előadáson szerepelt, hogy ez független az úttól (ezért lehet egyáltalán helyzeti energiáról beszélni), ezért egyszerűen Mennyinek válasszuk
-ba visszük a tömegpontot. Előadáson szerepelt, hogy ez független az úttól (ezért lehet egyáltalán helyzeti energiáról beszélni), ezért egyszerűen Mennyinek válasszuk![\[E_h = \int_{r}^{r_0} - \gamma \frac{m M}{r'^2} dr' = \left[ \gamma \frac{m M}{r'} \right]_{r}^{r_0} = + \gamma \frac{m M}{r_0} - \gamma \frac{m M}{r} \; .\]](/images/math/5/2/0/52014272eeb32d89657e9e5d03db2bab.png)
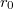 -t? Látható, ha
-t? Látható, ha 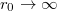 , akkor az első tag eltűnik, így ez egy kényelmes választás, és ez is a szokás. Azaz
, akkor az első tag eltűnik, így ez egy kényelmes választás, és ez is a szokás. Azaz ![\[E_h = - \gamma \frac{m M}{r} \, .\]](/images/math/1/3/2/1322391d8c3fa21df16cc9f1f0ddbea3.png)
- Nem adtuk meg
 -t és
-t és  -et, de tudjuk, hogy a Föld felszínén ebből
-et, de tudjuk, hogy a Föld felszínén ebből![\[\gamma \frac{m M}{R^2} = m g_0 \, ,\]](/images/math/0/d/9/0d9dc06a2a0f95140bc7fb43897fbd1c.png)
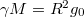 . Ezzel
. Ezzel ![\[E_h = - \frac{m R^2 g_0}{r} \; .\]](/images/math/3/2/2/3227148017774ccc84a8cd0ffe91af74.png)
- Egy test akkor hagyhatja el a Föld gravitációs terét, ha az összenergiája (mozgási + helyzeti) elegendő ahhoz, hogy végtelen messze távolodhasson a Földtől. Mivel a helyzeti energia nulla szintjét a végtelenben vettük fel, ezért ez azzal ekvivalens, hogy az összenergiának pozitívnak kell lennie. A Föld felszínén (
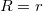 ) felírva ezt a feltételt, a második kozmikus sebességre ebből
) felírva ezt a feltételt, a második kozmikus sebességre ebből![\[ 0 = E = E_m + E_h = \frac{1}{2} m v_{2}^2 - \frac{m R^2 g_0}{R} \; ,\]](/images/math/5/c/6/5c6e98a6733999a469b9a9e79b6999e0.png)
![\[v_{2} = \sqrt{2 g_0 R} \approx 11.2 \, km/s \; .\]](/images/math/9/5/3/95370264f7b2cdb4a313e11bdc894ab5.png)
- a.) A felszínen a gravitációs gyorsulás