Magnetosztatika példák - Áramvezető elrendezésekre ható mágneses erőhatás
Feladat
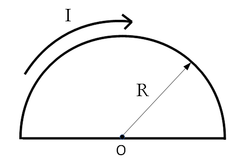
- Az ábrán látható két elrendezésnél mekkora az
 pont körüli nagyon kis
pont körüli nagyon kis 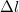 szakaszra ható erő, ha az áramerősség
szakaszra ható erő, ha az áramerősség  ?
?
a) az a.) ábrán a kör sugara
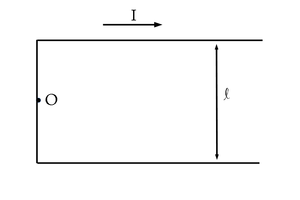
b) a b.) ábrán a párhuzamos vezetékek igen hosszúak, távolságuk
Megoldás
a.) Határozzuk meg a körív mágneses indukció vektorát az  pontban! A 6. feladatsor 7. feladatában már meghatároztuk egy
pontban! A 6. feladatsor 7. feladatában már meghatároztuk egy  sugarú,
sugarú,  árammal átjárt
árammal átjárt  szög alatt látszó körív alakú vezeték mágneses terét a körív középpontjában:
szög alatt látszó körív alakú vezeték mágneses terét a körív középpontjában:
![\[B=\dfrac{\mu_0 I}{4 \pi R}\alpha\]](/images/math/c/e/d/ced717de43545af6699009eb3dba3bbd.png)
Jelen esetben félkörről van szó, tehát a mágneses tér:
![\[B=\dfrac{\mu_0 I}{4 R}\]](/images/math/f/2/2/f221f3b530f81abf8c023f23776713cc.png)
A mágneses indukció vektora merőleges a keret síkjára, iránya az ábra síkjára merőlegesen befelé mutat.
A félkört lezáró egyenes vezető szakasz nem kelt mágneses teret az  pontban, hiszen a vezetőre fektetett egyenes átmegy az
pontban, hiszen a vezetőre fektetett egyenes átmegy az  ponton. Tehát a hurok mágneses tere az
ponton. Tehát a hurok mágneses tere az  pontban:
pontban:
![\[B=\dfrac{\mu_0 I}{4 R}\]](/images/math/f/2/2/f221f3b530f81abf8c023f23776713cc.png)
Az  pont
pont 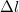 kis környezetében ezt a teret homogénnek tekintjük, így a vezető darabkára ható Lorentz erő:
kis környezetében ezt a teret homogénnek tekintjük, így a vezető darabkára ható Lorentz erő:
![\[\vec{F}=I(\vec{\Delta l}\times \vec{B})\]](/images/math/5/1/1/511250faa447a024932c1610b8227783.png)
A vektorszorzatot a vektorok ortogonalitása miatt átírhatjuk a mennyiségek algebrai szorzatára. Így megkapjuk az erő nagyságát:
![\[F=\dfrac{\mu_0 I^2 \Delta l}{4 R}\]](/images/math/7/6/e/76e1f10cb04de136ae533250131b5c97.png)
Belátható, hogy az erő vektora az ábra síkjában van, merőleges az egyenes vezetőre, és a félkörívvel átellenes irányba mutat.
b.) Az  pontban mérhető mágneses tér meghatározásakor három egyenes vezető által keltett teret kell összegeznünk. Az
pontban mérhető mágneses tér meghatározásakor három egyenes vezető által keltett teret kell összegeznünk. Az  ponton átmenő
ponton átmenő  hosszúságú vezetékdarab járuléka nulla, hasonló okokból, mint az a.) feladatban szereplő egyenes vezető esetén
Két félegyenes terét kell csak meghatároznunk. Véges hosszúságú áramjárta egyenes vezető terét már meghatároztuk a 6. feladatsor 1. feladatában.
hosszúságú vezetékdarab járuléka nulla, hasonló okokból, mint az a.) feladatban szereplő egyenes vezető esetén
Két félegyenes terét kell csak meghatároznunk. Véges hosszúságú áramjárta egyenes vezető terét már meghatároztuk a 6. feladatsor 1. feladatában.
![\[B=\dfrac{\mu_0 I}{4 \pi t} (\sin(\alpha_1)-\sin(\alpha_2))\]](/images/math/d/9/2/d92576e66b717790614891fc128109bb.png)
Ahol  a vizsgált pont és a vezetődarab távolsága,
a vizsgált pont és a vezetődarab távolsága, 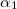 és
és 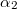 pedig a rúd két végpontjának látószöge a vizsgált pontból a vezetékhez húzott merőlegeshez képest. Nézzük a b. ábra 'felső' félegyenesét! Az
pedig a rúd két végpontjának látószöge a vizsgált pontból a vezetékhez húzott merőlegeshez képest. Nézzük a b. ábra 'felső' félegyenesét! Az  pont távolsága a vezetőtől:
pont távolsága a vezetőtől: 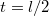 . Mivel a vezető szakasz egyik irányban végtelen hosszú, így
. Mivel a vezető szakasz egyik irányban végtelen hosszú, így 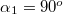 határértéket veszi fel. Mivel a félegyenes végpontja épp egybe esik az
határértéket veszi fel. Mivel a félegyenes végpontja épp egybe esik az  pontból az egyenesre állított merőleges talppontjával, ezért
pontból az egyenesre állított merőleges talppontjával, ezért 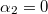 . A 'felső' áramjárta félegyenes által létrehozott tér nagysága tehát:
. A 'felső' áramjárta félegyenes által létrehozott tér nagysága tehát:
![\[B_1=\dfrac{\mu_0 I}{2 \pi l} (\sin(90^o)-\sin(0^o))=\dfrac{\mu_0 I}{2 \pi l}\]](/images/math/2/4/5/2452fefc906f58dd2071c7e6bf7471c1.png)
Ne feledjük, hogy a fenti összefüggést a Biot-Savart törvényből vezettük le, így az abban szereplő vektorszorzat segítségével beláthatjuk, hogy a 'felső' félegyenes az  pontban az ábra síkjára merőleges, befelé mutató indukciót hoz létre. A fentiekhez hasonlóan az is belátható, hogy az 'alsó' félegyenes a 'felsővel' azonos nagyságú és irányú teret hoz létre az
pontban az ábra síkjára merőleges, befelé mutató indukciót hoz létre. A fentiekhez hasonlóan az is belátható, hogy az 'alsó' félegyenes a 'felsővel' azonos nagyságú és irányú teret hoz létre az  pontban. Tehát a hurok által keltett teljes tér az
pontban. Tehát a hurok által keltett teljes tér az  pontban:
pontban:
![\[B=2B_1=\dfrac{\mu_0 I}{ \pi l}\]](/images/math/7/e/c/7ec6951db9c57b3f5a66d11d6da174fb.png)
Ebben a térben a 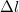 hosszúságú vezető szakaszra ható erő:
hosszúságú vezető szakaszra ható erő:
![\[\vec{F}=I(\vec{\Delta l}\times \vec{B})\]](/images/math/5/1/1/511250faa447a024932c1610b8227783.png)
A vektorszorzat alapján megállapítható, hogy a Lorentz erő az ábra síkjában hat, a 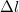 szakaszra merőlesen, a félegyenesekkel átellenenes irányba mutat.
szakaszra merőlesen, a félegyenesekkel átellenenes irányba mutat.
Az erő nagysága:
![\[\vec{F}=2B_1 I \Delta l=\dfrac{\mu_0 I^2 \Delta l}{ \pi l}\]](/images/math/2/a/e/2aef22b93f810ec6a26fe469ee945c7d.png)
Megjegyzés: A fenti két példa jól illusztrálja, hogy az áramjárta vezető hurkokra az önmaguk által keltett mágneses térben mindig olyan Lorentz erő hat, mely a hurkot tágítani, szétvetni kívánja.