Munka, energia - 2.2.1
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. április 13., 10:22-kor történt szerkesztése után volt.
Feladat
- Egy gépkocsi tömege
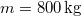 . Indulás után
. Indulás után 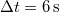 ideig gyorsít
ideig gyorsít 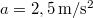 gyorsulással. Mekkora az átlagteljesítmény a
gyorsulással. Mekkora az átlagteljesítmény a  idő alatt? Írjuk fel a pillanatnyi teljesítményt, mint az idő függvényét! Számítsuk ki a teljesítmény legnagyobb értékét! (A súrlódástól eltekintünk.)
idő alatt? Írjuk fel a pillanatnyi teljesítményt, mint az idő függvényét! Számítsuk ki a teljesítmény legnagyobb értékét! (A súrlódástól eltekintünk.)
Megoldás
- A gyorsítás végén a test sebessége
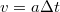 , a mozgási energiája pedig Az átlagos teljesítmény ez alapján
, a mozgási energiája pedig Az átlagos teljesítmény ez alapján![\[E_{kin}=\frac{1}{2}mv^{2}=\frac{1}{2}ma^{2}\Delta t^{2}\,.\]](/images/math/7/9/e/79eec82b6a187b41946a1f8cb6a70771.png) Az idő függvényében a kinetikus energia
Az idő függvényében a kinetikus energia![\[P=\frac{E_{kin}}{\Delta t}=\frac{1}{2}ma^{2}\Delta t=15000\,\mathrm{W}\,.\]](/images/math/3/a/7/3a7434d5183ae9235c1bfa7f17dd7d06.png)
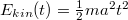 , amely alapján a teljesítmény az idő függvényében amely maximális értékét
, amely alapján a teljesítmény az idő függvényében amely maximális értékét![\[P(t)=\frac{dE_{kin}(t)}{dt}=ma^{2}t\,,\]](/images/math/e/c/5/ec5abb052b5f878475e816bc83777ac1.png)
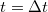 -nél veszi fel
-nél veszi fel 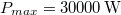 .
.
- A gyorsítás végén a test sebessége