Munka, energia - 2.2.14

Feladat

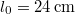1. Egy $\setbox0\hbox{$M$}% \message{//depth:\the\dp0//}% \box0%$ tömegű testet rugalmas fonal B végére erősítünk. A fonal $\setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0%$ vége rögzített, nyújtatlan állapotban $\setbox0\hbox{$l_{0}=24\,\mathrm{cm}$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú, és akkor tart 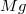$\setbox0\hbox{$Mg$}% \message{//depth:\the\dp0//}% \box0%$ erővel egyensúlyt, ha megnyúlása 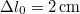$\setbox0\hbox{$\Delta l_{0}=2 \,\mathrm{cm}$}% \message{//depth:\the\dp0//}% \box0%$. A test kezdetben az A pontban áll, azután elengedjük, úgyhogy szabadon esik mindaddig, amíg a fonal engedi, azután a fonal elkezd nyúlni, eközben fékezi a test esését, végül meg is állítja. Tegyük fel, hogy a fonal megnyúlásával arányos erőt fejt ki a végére kötött testre. Mekkora lesz a fonal maximális megnyúlása?

Megoldás

1. A rugalmas fonal rugóállandóját 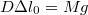$\setbox0\hbox{$D\Delta l_{0}=Mg$}% \message{//depth:\the\dp0//}% \box0%$ alapján számolhatjuk ki. A test leesése során a helyzeti energiája teljes egészében rugalmas energiává alakul, mert sem kezdetben, sem a végállapotban nincs mozgási energiája.

   $\[E_{h}=E_{rug}\]$

   $\[Mg(l_{0}+\Delta l)=\frac{1}{2}D\Delta l^{2}\,,\]$

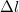   ahol $\setbox0\hbox{$\Delta l$}% \message{//depth:\the\dp0//}% \box0%$-lel jelöltük a fonál végső megnyúlását. A másodfokú egyenletnek két megoldása van:

   $\[\Delta l=\Delta l_{0}\left[1\pm\sqrt{1+\frac{2l_{0}}{\Delta l_{0}}}\right]\]$

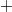   A két megoldás közül fizikailag csak a $\setbox0\hbox{$+$}% \message{//depth:\the\dp0//}% \box0%$ előljelű érdekes.

   $\[\Delta l=\Delta l_{0}\left[1+\sqrt{1+\frac{2l_{0}}{\Delta l_{0}}}\right]=12\,\mathrm{cm}\]$