Termodinamika példák - Keveredési entrópia, Gibbs-paradoxon
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Entrópia, II. főtétel |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egymástól válaszfallal elzárt,
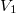 és
és 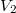 térfogatú két edényben azonos hőmérsékletű, azonos nyomású,
térfogatú két edényben azonos hőmérsékletű, azonos nyomású, 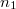 és
és 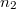 mólszámú, különböző fajtájú ideális gáz van. Ha a válaszfalat eltávolítjuk, akkor a két gáz összekeveredik.
mólszámú, különböző fajtájú ideális gáz van. Ha a válaszfalat eltávolítjuk, akkor a két gáz összekeveredik.
- a) Indokoljuk meg, hogy a folyamatban miért nem változik a hőmérséklet és a nyomás!
- b) Határozzuk meg az entrópia-változást (az ún. keverési entrópiát), és fejezzük ki a gázok
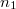 és
és 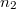 mólszámaival!
mólszámaival!
- c) Számítsuk ki az entrópia-változást, ha a két edényben azonos fajtájú gáz van!
Megoldás
a) A két edény paramétereit alsó indexek számokkal (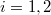 ), a gázokat betűkkel (
), a gázokat betűkkel (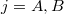 ) különböztetjük meg. Kezdetben az állapotegyenletek:
) különböztetjük meg. Kezdetben az állapotegyenletek:
![\[ p V_1= N_A kT \qquad\text{és}\qquad p V_2= N_B kT. \]](/images/math/8/f/f/8ffb0e148f2b73f12672f4fb1aeb1aa0.png)
A fal elvétele után a Dalton-törvényt felhasználva a kialakuló parciális nyomások:
![\[ p_A=\frac{N_A kT} {V_1+ V_2} \qquad\text{és}\qquad p_B=\frac{N_B kT} {V_1+ V_2},\]](/images/math/9/7/4/97484cad0cee1f0c0589fd2435acf033.png)
illetve a 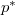 össznyomás
össznyomás
![\[ p^* = p_1+p_2 = \frac{N_A kT + N_B kT}{V_1+ V_2} = \frac{p V_1 + p V_2}{V_1+ V_2} = p. \]](/images/math/4/7/3/4730c8124db74341d7193acc1f52f02d.png)
b) Az első főtételt kiintegrálva korábban megkaptuk az entrópia hőmérséklet- és térfogatfüggését:
![\[ \Delta S_j = n_j C_{Vj} \ln\frac{T_{j\text{vég}}}{T_{j\text{kezd}}} +n_j R \ln\frac{V_{j\text{vég}}}{V_{j\text{kezd}}}, \]](/images/math/b/0/f/b0f51b192980c16371c16c6dd60154f3.png)
most 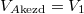 ,
, 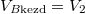 és
és 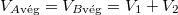 .
.
A hőmérséklet végig állandó (az a) részben azt láttuk be, hogy a kezdeti- és a végállapotban ugyanaz, a feladat megoldásához ez is elegendő). Ezeket felhasználva a két gáz entrópia-változásának összege
![\[ \Delta S = k\left(N_A \ln\frac{V_1+V_2}{V_1}+ N_B\ln \frac{V_1+V_2}{V_2}\right). \]](/images/math/5/9/9/5997be5001db6d5689452ea56a0d64ab.png)
A térfogatokat megkaphatjuk az állapotegyenletből,
![\[ V_1=\frac{n_A RT} p \qquad\text{és}\qquad V_2=\frac{n_B RT} p,\]](/images/math/2/c/e/2ceb58cf658463861a6261846b8e10fe.png)
így
![\[ \Delta S = R \left( n_A \ln\frac{n_A+n_B}{n_A}+ n_B \ln\frac{n_A+n_B}{n_B}\right)>0, \]](/images/math/2/d/9/2d99565e6f44a47a8c5023b9e3c7bf54.png)
ami a feladatban adott 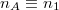 és
és 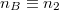 értékekkel
értékekkel
![\[ \Delta S = R \left( n_1 \ln\frac{n_1+n_2}{n_1}+ n_2 \ln\frac{n_1+n_2}{n_2}\right)>0. \]](/images/math/3/7/5/3755081c693f99bf4c4e41631fac60d8.png)
c) Ha a két edényben azonos gáz van, akkor bármelyik pillanatban munkavégzés nélkül visszatehetjük a válaszfalat és ugyanúgy az egyensúlyi kezdeti makroállapotot kapjuk eredményként, az entrópia nem változhatott meg:
![\[ \Delta S = 0, \]](/images/math/9/c/4/9c42fd9c23c5c5501663b1d6c7b963bb.png)
noha a b) pontban kapott eredmény az entrópia növekedését sugallná, ez a Gibbs-paradoxon.
Megjegyzés: a Gibbs-paradoxon
Az eltérés a klasszikus részecskeképben és az entrópia definíciójában keresendő: a végállapot entrópiájának számításakor feltettük, hogy meg tudjuk különböztetni, kezdetben melyik részecske melyik tartályban volt, ami különböző anyagi minőségű gázok esetén lehetséges is. A kvantummechanika eredményei szerint viszont az azonos anyagi minőségű részecskék megkülönböztethetetlenek, azaz miután egyetlen közös térbe engedtük őket, elméletben sincs olyan mérés, ami egyszerre megmondja a kezdőfeltételeket (a részecskék pontos sebességét és pontos helyét), sem olyan, amelyik megmondja, melyik részecske eredetileg melyik tartályban volt.
Tekintsük most az entrópia Boltzmann-féle definícióját:
![\[ S = k \ln W, \]](/images/math/e/8/c/e8c712fad5345992cd44310ac103ec0d.png)
ahol 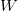 a makroállapotot megvalósító lehetséges mikroállapotok száma.
A kezdeti állapotban a mikroállapotok száma a két edény mikroállapotai számának szorzata, hiszen a két edény egymástól független rendszer:
a makroállapotot megvalósító lehetséges mikroállapotok száma.
A kezdeti állapotban a mikroállapotok száma a két edény mikroállapotai számának szorzata, hiszen a két edény egymástól független rendszer:
![\[ W_\text{kezd} = W_1 \cdot W_2, \]](/images/math/c/0/c/c0cd8a6abc94b81c771a32bccbb5e3fb.png)
a végállapotot jelölje 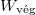 , amikkel:
, amikkel:
![\[ \Delta S = k\ln\frac{W_\text{vég}}{W_\text{kezd}}. \]](/images/math/8/4/0/8402c97aba0c7e289fc145d53c75c80c.png)
A b) pontban kapott eredményt 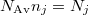 összefüggéessel átírva részecskeszámokra
összefüggéessel átírva részecskeszámokra
![\[ \Delta S = k \left( N_A \ln\frac{N_A+N_B}{N_1}+ N_B \ln\frac{N_A+N_B}{N_B}\right)>0, \]](/images/math/0/3/9/0390476526620c4545f33cb7d2794e53.png)
ahol 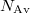 az Avogadro-,
az Avogadro-,  pedig a Boltzmann-állandó.
pedig a Boltzmann-állandó.
A Boltzmann-féle entrópiadefiníciót ki kell egészítenünk a megkülönböztethetetlenséggel, azaz azonos anyagi minőségű részecskék permutációja nem vezet új makroállapothoz:
![\[ S^* = k \ln W^* = k \ln\frac{W}{\prod_j N_j!}, \]](/images/math/5/2/d/52d6663fcf5b826ffc30a42a71a426a9.png)
amivel különböző fajtájú gázokra ![\[ \Delta S^* = k\ln\frac{W^*_\text{vég}}{W^*_\text{kezd}} = k\ln \left( \frac{W_\text{vég}}{W_1 W_2} \frac{N_A!N_B!}{N_A!N_B!} \right), \]](/images/math/f/c/f/fcf11c375c305b8e55fcb3e56dba81fa.png) 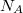 és és 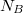 az egyes gázok részecskeszáma, az egyes gázok részecskeszáma,
|
és azonos fajtájú gázra ![\[ \Delta S^* = k\ln\frac{W^*_\text{vég}}{W^*_\text{kezd}} = k\ln \left( \frac{W_\text{vég}}{W_1 W_2} \frac{N_1!N_2!}{(N_1+N_2)!} \right), \]](/images/math/e/2/2/e22efc560e124386e171e35aa65eb18d.png) 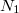 és és 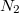 a tartályok kezdeti (egyben egyensúlyi) részecskeszáma. a tartályok kezdeti (egyben egyensúlyi) részecskeszáma.
|
A Stirling-formula (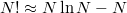 ) segítségével
) segítségével
![\[ \ln \frac{N_1!N_2!}{(N_1+N_2)!} \approx N_1 \ln N_1 - N_1 + N_2 \ln N_2 - N_2 - (N_1+N_2) \ln (N_1+N_2) + (N_1+N_2) = N_1 \ln \frac{N_1}{N_1+N_2} + N_2 \ln \frac{N_2}{N_1+N_2}, \]](/images/math/1/c/0/1c0a26c4b739c9bbc31e51e1aa3244bd.png)
azaz különböző fajtájú gázokra ![\[ \Delta S^* = \Delta S = k \left( N_A \ln\frac{N_A+N_B}{N_1}+ N_B \ln\frac{N_A+N_B}{N_B}\right)>0, \]](/images/math/4/f/5/4f537c2c7e982ccdc5899e40716feddc.png) |
és azonos fajtájú gázra ![\[ \Delta S^* = \Delta S \cdot \left(N_1 \ln \frac{N_1}{N_1+N_2} + N_2 \ln \frac{N_2}{N_1+N_2}\right) = \ln 1 = 0, \]](/images/math/2/a/3/2a37d6fa5310a521489e87ac6464b8d7.png) |
Megjegyzés más levezetésekhez
Találkozhatunk olyan levezetéssel, ami a tartályokat további képzeletbeli egységekre bontja, és a azonos fajtájú gázra számszerűen helyes eredményt ad. Ezt a levezetést alább közöljük, de kevésbé ajánljuk, mert nem tisztázza a megkülönböztethetetlenség kérdését, ugyanakkor a formalizmust feleslegesen bonyolítja.
Legyen azonos fajtájú gáz van mindkét tartályban, a Boltzmann-féle entrópiával számolunk.
Az első tartályt  , a másodikat
, a másodikat  darab cellára osztjuk fel, amelyekben rendre
darab cellára osztjuk fel, amelyekben rendre 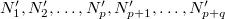 részecske van. Ezt a makroállapotot a fal elvétele előtt
részecske van. Ezt a makroállapotot a fal elvétele előtt 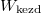 -féle mikroállapot valósíthatja meg. Az
-féle mikroállapot valósíthatja meg. Az 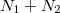 darab részecskét – mivel azok azonos fajtájúak – a két edényben rendelkezésre álló
darab részecskét – mivel azok azonos fajtájúak – a két edényben rendelkezésre álló 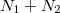 helyükre
helyükre 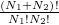 -féleképpen oszthatjuk szét. Majd ezeket az adott edényükben levő cellákban is szét kell osztanunk:
-féleképpen oszthatjuk szét. Majd ezeket az adott edényükben levő cellákban is szét kell osztanunk:
![\[ W_\text{kezd} = \frac{\left( N_1+ N_2\right)!}{N_1! N_2!}\cdot \frac{N_1!}{\prod_{i=1}^p N'_i!}\cdot \frac{N_2!}{\prod_{i=p+1}^{p+q} N'_i!} =\frac{\left( N_1+ N_2\right)!}{\prod _{i=1}^{p+q} N'_i!}. \]](/images/math/8/f/3/8f3454aa90d9d940c56837b0a93c52f7.png)
A fal felnyitását követően is osszuk fel az egybenyitott edényeket az előbbi makroállapotnak megfelelően (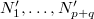 ). Ekkor a
). Ekkor a 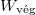 termodinamikai valószínűség:
termodinamikai valószínűség:
![\[ W_\text{vég} = \frac{\left( N_1+ N_2\right)!}{\prod _{i=1}^{p+q} N'_i!}.\]](/images/math/9/8/8/9889874ce65699b6f64c7ee6379542aa.png)
Ezekkel a Boltzmann-féle entrópia:
![\[ \Delta S = k\ln \frac{W_\text{vég}}{W_\text{kezd}} = 0. \]](/images/math/6/0/9/60986ac21ccf9d6669bf4c2d6369f280.png)
Ha kezdetben a két edényben különböző gázok volnának, akkor 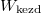 -ben az
-ben az 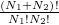 tényező eltűnne, hiszen csak egyféleképpen tudnánk szétosztani a részecskéket a tartályok között, míg
tényező eltűnne, hiszen csak egyféleképpen tudnánk szétosztani a részecskéket a tartályok között, míg 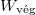 változatlan maradna. Ekkor:
változatlan maradna. Ekkor:
![\[ \Delta S = k\ln \frac{W_\text{vég}}{W_\text{kezd}} = k\ln \frac{\left( N_1+ N_2\right)!}{N_1! N_2!}. \]](/images/math/d/1/6/d16e9bccdcbe981df049bca5c6f35d47.png)
Vegyük észre, hogy a fal felnyitása előtt és után ugyanannyi részecske volt az egyes képzeletbeli cellákban, ez csak egyensúlyban, makroszkopikusan nagy cellákra igaz. Vegyük még észre, hogy élhetünk a 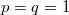 választással, ekkor azonos fajtájú gázra
választással, ekkor azonos fajtájú gázra 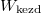 és
és 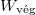 már az egyszerűsítés előtt ugyanazt az alakot ölti, ami a gázrészecskék egymás közötti teljes felcserélhetőségére utal, ami a kezdőállapotban kvantummechanikailag nem is igaz; különböző fajtájú gázokra
már az egyszerűsítés előtt ugyanazt az alakot ölti, ami a gázrészecskék egymás közötti teljes felcserélhetőségére utal, ami a kezdőállapotban kvantummechanikailag nem is igaz; különböző fajtájú gázokra 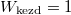 és
és 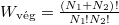 , amit könnyebben magyarázhatunk a megkülönböztethetőséggel.
, amit könnyebben magyarázhatunk a megkülönböztethetőséggel.
Tehát érdemesebb a legelőször bemutatott, kvantummechanikai alapokon nyugvó levezetést használni.