| [rejt] Navigáció Pt·1·2·3
|
| Kísérleti fizika gyakorlat 2.
|
Gyakorlatok listája:
- Erőhatások elektromos erőtérben, elektromos térerősség
- Elektromos potenciál
- Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok
- Kapacitás, kondenzátorok. Elrendezések energiája
- Vezetőképesség, áramsűrűség
- Biot-Savart törvény, gerjesztési törvény
- Erőhatások mágneses térben
- Mágneses térerősség. Kölcsönös és öninduktivitás
- Az indukció törvénye, mozgási indukció
- Mágneses tér energiája. Váltakozó áram, eltolási áram
|
| Magnetosztatika - Mágneses tér energiája. Váltakozó áram, eltolási áram
|
Feladatok listája:
- Toroid energiája
- Légrésben és a vasmagban tárolt energia
- Tranziens jelenség LR körben
- Fáziskésés váltakozó-áramú LR körben
- Eltolási áram síkkondenzátorban
- Váltakozó áramra kapcsolt síkkondenzátorban a térerősség
- Eltolási áramsűrűség szolenoidban
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064
|
Feladat
- Határozzuk meg, mekkora az eltolási áram egy olyan síkkondenzátor esetén, amelynek lemezei egymással párhuzamosak maradnak, miközben
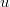 sebességgel távolodnak egymástól, ha
sebességgel távolodnak egymástól, ha
a) az  töltéssűrűség állandó
töltéssűrűség állandó
b) a lemezek közötti feszültség állandó.
Megoldás
a, Mivel  állandó, ezért a
állandó, ezért a  elektromos eltolás nagysága is állandó a kondenzátor lemezei között. Az eltolási áram értéke tehát zérus. Vagyis:
elektromos eltolás nagysága is állandó a kondenzátor lemezei között. Az eltolási áram értéke tehát zérus. Vagyis:
b, Ha kondenzátor lemezei között az  feszültség állandó, akkor:
feszültség állandó, akkor:
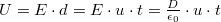 Amiből az elektomos eltolás nagysága:
Amiből az elektomos eltolás nagysága:
Az etolási áram pedig:
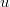 sebességgel távolodnak egymástól, ha
sebességgel távolodnak egymástól, ha  töltéssűrűség állandó
töltéssűrűség állandó  állandó, ezért a
állandó, ezért a  elektromos eltolás nagysága is állandó a kondenzátor lemezei között. Az eltolási áram értéke tehát zérus. Vagyis:
elektromos eltolás nagysága is állandó a kondenzátor lemezei között. Az eltolási áram értéke tehát zérus. Vagyis:
![\[\frac{\partial D}{\partial t} = 0\]](/images/math/1/c/c/1cc2bd06331a5f4b5abd0bb327a36516.png)
 feszültség állandó, akkor:
feszültség állandó, akkor:
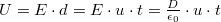 Amiből az elektomos eltolás nagysága:
Amiből az elektomos eltolás nagysága:
![\[D = \frac{\epsilon_0 U}{ut}\]](/images/math/0/9/b/09b52911ae0d981b405d57a99440edf7.png)
![\[\frac{\partial D}{\partial t} = -\frac{U \epsilon_0}{ut^2}\]](/images/math/0/b/4/0b4c599dac950846ccaeceb05815b655.png)