Magnetosztatika példák - Szolenoid mágneses tere 2. (Biot-Savart)
Feladat
- Határozzuk meg a mágneses indukció nagyságát egy
 sugarú,
sugarú,  hosszúságú,
hosszúságú,  menetű szolenoidban, amelyben
menetű szolenoidban, amelyben  áram folyik, Biot-Savart törvény segítségével.
áram folyik, Biot-Savart törvény segítségével.
Megoldás
Éljünk azzal a közelítéssel, hogy a szolenoid nem tekercs, hanem egy folytonos vezető hengerpalást, melyben összesen 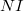 áram folyik egyenletes
áram folyik egyenletes  felületi áramsűrűséggel, a henger palástján körbefutó köráramok formájában.
Határozzuk meg a
felületi áramsűrűséggel, a henger palástján körbefutó köráramok formájában.
Határozzuk meg a  felületi áramsűrűség nagyságát:
felületi áramsűrűség nagyságát:
![\[j=\dfrac{NI}{l}\]](/images/math/e/d/7/ed7f54a29072fd7903a5f91c0ce2905e.png)
Essen egybe a szolenoid tengelye a koordinátarendszer  tengelyével, a szolenoid középpontja pedig az origóval! Bontsuk fel a szolenoidot modellező hengerpalástunkat
tengelyével, a szolenoid középpontja pedig az origóval! Bontsuk fel a szolenoidot modellező hengerpalástunkat 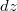 szélességű elemi gyűrűkre. Egy elemi gyűrűben folyó
szélességű elemi gyűrűkre. Egy elemi gyűrűben folyó 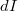 áram nagysága:
áram nagysága:
![\[dI=jdz=\dfrac{NI}{l}dz\]](/images/math/7/b/4/7b4d534a3b4018a231b64c90973dae66.png)
A szolenoid terét meghatározhatjuk úgy, hogy a sok infinitezimális 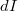 árammal átjárt
árammal átjárt  sugarú gyűrű által keltett teret összegezzük az origóban, vagyis a szolenoid középpontjában. A problémát az jelenti, hogy minden egyes köráram az origótól eltérő
sugarú gyűrű által keltett teret összegezzük az origóban, vagyis a szolenoid középpontjában. A problémát az jelenti, hogy minden egyes köráram az origótól eltérő  távolságra helyezkedik el. Szerencsére az
távolságra helyezkedik el. Szerencsére az  árammal átjárt,
árammal átjárt,  sugarú gyűrű terét ismerjük tengelyének minden pontjában a Körmozgást végző töltött test mágneses tere b.) feladatának megoldásából:
sugarú gyűrű terét ismerjük tengelyének minden pontjában a Körmozgást végző töltött test mágneses tere b.) feladatának megoldásából:
![\[B=\dfrac{\mu_0 I R^2}{2 (R^2+z^2)^{3/2}}\]](/images/math/6/3/c/63c6bf22be1f7f3b0ac668b4745c59ee.png)
Tehát a mi esetünkben az infinitezimális 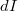 árammal átjárt gyűrű elemi indukció járuléka:
árammal átjárt gyűrű elemi indukció járuléka:
![\[dB=\dfrac{\mu_0 R^2}{2 (R^2+z^2)^{3/2}} dI=\dfrac{\mu_0 NI R^2}{2l (R^2+z^2)^{3/2}} dz\]](/images/math/0/c/6/0c67c929f0a23aba7737715fc14cd215.png)
A szolenoid középpontjában úgy kaphatjuk meg a teljes teret, ha az elemi áramgyűrűk terét felösszegezzük a szolenoid elejétől a végéig:
![\[B=\int dB=\dfrac{\mu_0 NI R^2}{2l} \int_{-l/2}^{l/2}\dfrac{1}{(R^2+z^2)^{3/2}} dz\]](/images/math/e/8/a/e8a7828ee4034404837d10350f3f3a84.png)
Az integrált kiszámolva:
![\[B=\dfrac{\mu_0 NI R^2}{2l} \left[ \dfrac{z}{R^2(R^2+z^2)^{1/2}} \right]_{-l/2}^{l/2}=\dfrac{\mu_0 NI}{\sqrt{4R^2+l^2}}\]](/images/math/9/9/1/9918f1ccd1d6c4321eab941e45e52bd4.png)
Megjegyzés:
Megoldásunkat érdemes összevetni a Szolenoid mágneses tere (Ampere-féle gerjesztés) feladatának eredményével, ahol az Amper-féle gerjesztési törvény segítségével vezettük le a szolenoid terének jól ismert formuláját:
![\[B=\dfrac{\mu_0 NI}{l}\]](/images/math/2/0/7/207641385b12448b0305980157b8c127.png)
Vegyük a jelen feladat eredményének azt a határesetét, amikor a tekercs  keresztmetszeti sugara elhanyagolható a tekercs
keresztmetszeti sugara elhanyagolható a tekercs  hosszához képest:
hosszához képest:
![\[\lim_{R/l \to 0}B=\lim_{R/l \to 0}\dfrac{\mu_0 NI}{\sqrt{4R^2+l^2}}=\dfrac{\mu_0 NI}{l}\]](/images/math/7/0/8/708e6805e1c5b648b091966e360e2b4f.png)
Tehát határértékben visszakapjuk a gerjesztési törvényből származó formulát. A fenti gondolatmenet azonban megmutatta, hogy alkalmazása csak akkor ad pontos eredményt, ha a tekercs keresztmetszete jóval kisebb, mint a hossza.