„Magnetosztatika példák - Vezető keret, mozgási indukicó” változatai közötti eltérés

A Fizipedia wikiből
(→‎Megoldás)
 
(egy szerkesztő 4 közbeeső változata nincs mutatva)
8. sor: 8. sor:
 
}}
 
}}
 
== Feladat ==
 
== Feladat ==
−
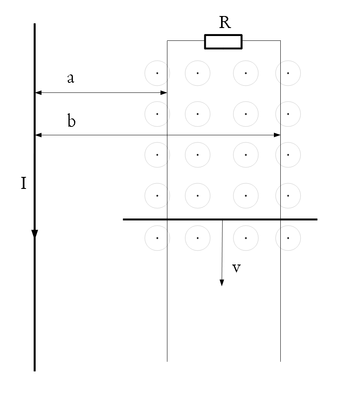
</noinclude><wlatex>#Egy végtelen hosszúnak tekinthető egyenes vezetőben $I$ áram folyik. A vezetőtől $a$ ill. $b$ távolságban vele párhuzamosan elhelyezett két vezető egyik vége egy $R$ ellenálláson keresztül össze van kötve. A két párhuzamos vezetőn, egy rájuk merőlegesen elhelyezett vezetőt csúsztatunk $v$ sebességgel. <br> '''a)''' Határozza meg a vezető keretben indukált áram irányát és nagyságát. (A vezetők ellenállása elhanyagolható) <br> '''b)''' Állapítja meg az az erőt, amely az állandó sebsség fenntartásához szükséges, valamint az $I$ áramot szállító vezetőtől azt az $x$ távolságot, ahol ennek az erőnek támadnia kell! <br> '''c)''' Határozza meg a vezető mozgatásához szükséges teljesítményt. <br> [[Kép:KFGY2-9-4.png|none|350px]] </wlatex><includeonly><wlatex>{{Végeredmény|content='''a)'''$$I_{ind} = \frac{U}{R} = - \frac{\mu_0 I v}{2\pi R}\ln\left(\frac{b}{a}\right)$$ <br> '''b)''' $$F = \int_a^b \frac{\mu_0 I_{ind} I}{2\pi r} dr = \frac{\mu_0 I_{ind} I}{2\pi}\ln\left(\frac{b}{a}\right)$$ $$x = \frac{(b-a)}{\ln\left(\frac{b}{a}\right)}$$ <br> '''c)''' $$P = \frac{\mu_0^2 I^2}{4\pi^2 R}\ln\left(\frac{b}{a}\right)^2 v^2 = U\cdot I$$ }}
+
</noinclude><wlatex>#Egy végtelen hosszúnak tekinthető egyenes vezetőben $I$ áram folyik. A vezetőtől $a$ ill. $b$ távolságban vele párhuzamosan elhelyezett két vezető egyik vége egy $R$ ellenálláson keresztül össze van kötve. A két párhuzamos vezetőn egy rájuk merőlegesen elhelyezett vezetőt csúsztatunk $v$ sebességgel. <br> '''a)''' Határozza meg a vezető keretben indukált áram irányát és nagyságát. (A vezetők ellenállása elhanyagolható) <br> '''b)''' Állapítsa meg az az erőt, amely az állandó sebesség fenntartásához szükséges, valamint az $I$ áramot szállító vezetőtől azt az $x$ távolságot, ahol ennek az erőnek támadnia kell! <br> '''c)''' Határozza meg a vezető mozgatásához szükséges teljesítményt. <br> [[Kép:KFGY2-9-4.png|none|350px]] </wlatex><includeonly><wlatex>{{Végeredmény|content='''a)'''$$I_{ind} = \frac{U}{R} = - \frac{\mu_0 I v}{2\pi R}\ln\left(\frac{b}{a}\right)$$ <br> '''b)''' $$F = \int_a^b \frac{\mu_0 I_{ind} I}{2\pi r} dr = \frac{\mu_0 I_{ind} I}{2\pi}\ln\left(\frac{b}{a}\right)$$ $$x = \frac{(b-a)}{\ln\left(\frac{b}{a}\right)}$$ <br> '''c)''' $$P = \frac{\mu_0^2 I^2}{4\pi^2 R}\ln\left(\frac{b}{a}\right)^2 v^2 = U\cdot I$$ }}
 
</wlatex></includeonly><noinclude>
 
</wlatex></includeonly><noinclude>
 +
 
== Megoldás ==
 
== Megoldás ==
 
<wlatex>
 
<wlatex>
16. sor: 17. sor:
 
A vezetőkeretben indukált feszültség a Faraday-féle indukciós törvény értelmében:
 
A vezetőkeretben indukált feszültség a Faraday-féle indukciós törvény értelmében:
 
$$U = -\frac{\partial \Phi}{\partial t} = -\frac{\partial}{\partial t} \int_a^b \frac{\mu_0 I}{2\pi r} vt dr = - \frac{\mu_0 I v}{2\pi}\ln\left(\frac{b}{a}\right) $$
 
$$U = -\frac{\partial \Phi}{\partial t} = -\frac{\partial}{\partial t} \int_a^b \frac{\mu_0 I}{2\pi r} vt dr = - \frac{\mu_0 I v}{2\pi}\ln\left(\frac{b}{a}\right) $$
−
Ezzel a vezetőkeretben folyó áram:
+
A vezetőkeretben induló áram:
 
$$I_{ind} = \frac{U}{R} = - \frac{\mu_0 I v}{2\pi R}\ln\left(\frac{b}{a}\right) $$
 
$$I_{ind} = \frac{U}{R} = - \frac{\mu_0 I v}{2\pi R}\ln\left(\frac{b}{a}\right) $$
  
−
Az áram olyan irányú lesz, hogy a vezetőkeret által létrehozott mágneses tér az egyenes vezető terével ellentétes irányú legyen. Mivel az ábra szerint az egyenes vezetőben lefele folyik az áram, ezért a vezető keretben az indukált áram az óra járásával megegyező irányban fog folyni.  
+
A vezetőkeretben indukált áram által létrehozott mágneses tér a egyenesvezető terével ellentétes irányú lesz a Lenz törvény értelmében. Mivel az ábra szerint az egyenes vezetőben lefelé folyik az áram, ezért a vezető keretben az indukált áram az óra járásával megegyező irányban fog folyni.  
  
−
b, A keretmozgatásához szükséges erő nagyságának meg kell egyezni a rudat visszahúzó Lorentz erő nagyságával. Hiszen a Lorentz erő a Lenz-törvény értelmében a keretben induklálódó áram olyan irányú, hogy a keret mozgásirányával ellentétes irányban hat.
+
b, A keret mozgatásához szükséges erő nagyságának meg kell egyeznie a rúdra ható Lorentz erő nagyságával. Mivel a rúd inhomogén mágneses térben mozog, a rúd elemi $dl$ szakaszaira más-más Lorentz erő hat:
−
$$\vec{F} = I_{ind} \int \vec{B} \times \vec{dl} $$
+
 
−
Mivel a mágneses tér mindenütt merőleges a vezetőkeretre:
+
$$d\vec{F} = I_{ind} \int \vec{B} \times \vec{dl} $$
 +
Mivel a mágneses tér mindenütt merőleges a rúdra, az eredő erő nagyságát megkaphatjuk az elemi szakaszokra ható Lorentz erők skaláris integrálásával. Tehát a rúd mozgatásához szükséges erő nagysága:
 
$$F = \int_a^b \frac{\mu_0 I_{ind} I}{2\pi r} dr = \frac{\mu_0 I_{ind} I}{2\pi}\ln\left(\frac{b}{a}\right)$$
 
$$F = \int_a^b \frac{\mu_0 I_{ind} I}{2\pi r} dr = \frac{\mu_0 I_{ind} I}{2\pi}\ln\left(\frac{b}{a}\right)$$
−
Mivel a nagyon hosszú egyenes vezető tere nem homogén mágneses teret hoz létre, ezért a vezető keretre ható Lorentz erő sem lesz egyenletes. Ezért a Lorentz erőnek  lesz eredő forgatónyomatéka.
+
 
−
A rúdat olyan a támadási pontban kell húzni, hogy annak forgatónyomatéka éppen kiejtse a Lorentz erő forgatónyomatékát.
+
 
−
Ha a csomópontot az egyenes vezetőhöz vesszük fel akkor a Lorentz erő forgatónyomatéka:
+
 
 +
Az húzóerő támadáspontját úgy kell megválasztanunk, hogy a húzóerő és a Lorentz erő rúdra kifejtett együttes forgatónyomatéka zérus legyen. Máskülönben a rúd elfordul, nem önmagával párhuzamosan mozdul el.
 +
 
 +
 
 +
 
 +
 +
A Lorentz erő forgatónyomatékát az alábbi integrállal határozhatjuk meg. :
 
$$M_L = \int_a^b \frac{\mu_0 I_{ind} I}{2\pi r} r dr = \frac{\mu_0 I_{ind} I}{2\pi}(b-a)$$
 
$$M_L = \int_a^b \frac{\mu_0 I_{ind} I}{2\pi r} r dr = \frac{\mu_0 I_{ind} I}{2\pi}(b-a)$$
−
A húzó erő forgatónyomatéka az $x$ pontban:
+
Ahol a forgástengelyt az I árammal átjárt egyenes vezetőn vettük fel.
 +
A húzó erő forgatónyomatékát felírva ugyanerre a tengelyre:
 
$$M_h = \frac{\mu_0 I_{ind} I}{2\pi}\ln\left(\frac{b}{a}\right) x$$
 
$$M_h = \frac{\mu_0 I_{ind} I}{2\pi}\ln\left(\frac{b}{a}\right) x$$
−
Ebből:
+
Ahol $x$ a támadáspont és az egyenes vezető távolsága.
 +
 
 +
A nyomatékok egyensúlyára felírt egyenletből kifejezhetjük a támadáspont vonalvezetőtől mért távolságát:
 
  $$M_h = M_L \rightarrow x = \frac{(b-a)}{\ln\left(\frac{b}{a}\right)}$$
 
  $$M_h = M_L \rightarrow x = \frac{(b-a)}{\ln\left(\frac{b}{a}\right)}$$
 
c, A vezető mozgatásához szükséges teljesítmény:
 
c, A vezető mozgatásához szükséges teljesítmény:

A lap jelenlegi, 2013. október 1., 15:26-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 2.
Gyakorlatok listája:
  1. Erőhatások elektromos erőtérben, elektromos térerősség
  2. Elektromos potenciál
  3. Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok
  4. Kapacitás, kondenzátorok. Elrendezések energiája
  5. Vezetőképesség, áramsűrűség
  6. Biot-Savart törvény, gerjesztési törvény
  7. Erőhatások mágneses térben
  8. Mágneses térerősség. Kölcsönös és öninduktivitás
  9. Az indukció törvénye, mozgási indukció
  10. Mágneses tér energiája. Váltakozó áram, eltolási áram
Magnetosztatika - Mozgási indukció
Feladatok listája:
  1. Forgó tekercsben indukált elektromotoros erő
  2. Parabola alakú vezetőben kialakult indukált feszültség
  3. Tekercsben indukált elektromotoros erő változó mágneses térben
  4. Vezető keret, mozgási indukicó
  5. Küllős fémtárcsában indukált elektromotoros erő
  6. V alakú sínen mozgó vezetőben indukált áram
  7. Lezárt sínen állandó erő erővel mozgatott vezető
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

  1. Egy végtelen hosszúnak tekinthető egyenes vezetőben \setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0% áram folyik. A vezetőtől \setbox0\hbox{$a$}% \message{//depth:\the\dp0//}% \box0% ill. \setbox0\hbox{$b$}% \message{//depth:\the\dp0//}% \box0% távolságban vele párhuzamosan elhelyezett két vezető egyik vége egy \setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0% ellenálláson keresztül össze van kötve. A két párhuzamos vezetőn egy rájuk merőlegesen elhelyezett vezetőt csúsztatunk \setbox0\hbox{$v$}% \message{//depth:\the\dp0//}% \box0% sebességgel.
    a) Határozza meg a vezető keretben indukált áram irányát és nagyságát. (A vezetők ellenállása elhanyagolható)
    b) Állapítsa meg az az erőt, amely az állandó sebesség fenntartásához szükséges, valamint az \setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0% áramot szállító vezetőtől azt az \setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0% távolságot, ahol ennek az erőnek támadnia kell!
    c) Határozza meg a vezető mozgatásához szükséges teljesítményt.
    KFGY2-9-4.png

Megoldás


a, Az egyenes vezető tere \setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0% távolságban:

\[B = \frac{\mu_0 I}{2\pi r}\]

A vezetőkeretben indukált feszültség a Faraday-féle indukciós törvény értelmében:

\[U = -\frac{\partial \Phi}{\partial t} = -\frac{\partial}{\partial t} \int_a^b \frac{\mu_0 I}{2\pi r} vt dr = - \frac{\mu_0 I v}{2\pi}\ln\left(\frac{b}{a}\right) \]

A vezetőkeretben induló áram:

\[I_{ind} = \frac{U}{R} = - \frac{\mu_0 I v}{2\pi R}\ln\left(\frac{b}{a}\right) \]

A vezetőkeretben indukált áram által létrehozott mágneses tér a egyenesvezető terével ellentétes irányú lesz a Lenz törvény értelmében. Mivel az ábra szerint az egyenes vezetőben lefelé folyik az áram, ezért a vezető keretben az indukált áram az óra járásával megegyező irányban fog folyni.

b, A keret mozgatásához szükséges erő nagyságának meg kell egyeznie a rúdra ható Lorentz erő nagyságával. Mivel a rúd inhomogén mágneses térben mozog, a rúd elemi \setbox0\hbox{$dl$}% \message{//depth:\the\dp0//}% \box0% szakaszaira más-más Lorentz erő hat:

\[d\vec{F} = I_{ind} \int \vec{B} \times \vec{dl} \]

Mivel a mágneses tér mindenütt merőleges a rúdra, az eredő erő nagyságát megkaphatjuk az elemi szakaszokra ható Lorentz erők skaláris integrálásával. Tehát a rúd mozgatásához szükséges erő nagysága:

\[F = \int_a^b \frac{\mu_0 I_{ind} I}{2\pi r} dr = \frac{\mu_0 I_{ind} I}{2\pi}\ln\left(\frac{b}{a}\right)\]



Az húzóerő támadáspontját úgy kell megválasztanunk, hogy a húzóerő és a Lorentz erő rúdra kifejtett együttes forgatónyomatéka zérus legyen. Máskülönben a rúd elfordul, nem önmagával párhuzamosan mozdul el.




A Lorentz erő forgatónyomatékát az alábbi integrállal határozhatjuk meg. :

\[M_L = \int_a^b \frac{\mu_0 I_{ind} I}{2\pi r} r dr = \frac{\mu_0 I_{ind} I}{2\pi}(b-a)\]

Ahol a forgástengelyt az I árammal átjárt egyenes vezetőn vettük fel. A húzó erő forgatónyomatékát felírva ugyanerre a tengelyre:

\[M_h = \frac{\mu_0 I_{ind} I}{2\pi}\ln\left(\frac{b}{a}\right) x\]

Ahol \setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0% a támadáspont és az egyenes vezető távolsága.

A nyomatékok egyensúlyára felírt egyenletből kifejezhetjük a támadáspont vonalvezetőtől mért távolságát:

\[M_h = M_L \rightarrow x = \frac{(b-a)}{\ln\left(\frac{b}{a}\right)}\]

c, A vezető mozgatásához szükséges teljesítmény:

\[P = F\cdot v = \frac{\mu_0 I_{ind} I}{2\pi}\ln\left(\frac{b}{a}\right) v = \frac{\mu_0^2 I^2}{4\pi^2 R}\ln\left(\frac{b}{a}\right)^2 v^2 = U\cdot I\]

Vagyis a vezető mozgatásához szükséges teljesítmény megegyezik az áramkörben disszipált elektromos teljesítménnyel.


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Magnetosztatika_példák_-_Vezető_keret,_mozgási_indukicó&oldid=13141”