„Termodinamika példák - Keveredési entrópia, Gibbs-paradoxon” változatai közötti eltérés

A Fizipedia wikiből
13. sor: 13. sor:
 
#* b) <wlatex>Határozzuk meg az entrópia-változást (az ún. keverési entrópiát), és fejezzük ki a gázok $n_1$ és $n_2$ mólszámaival!
 
#* b) <wlatex>Határozzuk meg az entrópia-változást (az ún. keverési entrópiát), és fejezzük ki a gázok $n_1$ és $n_2$ mólszámaival!
 
</wlatex><includeonly><wlatex>{{Útmutatás|content=Alkalmazzuk az [[Termodinamika példák - Ideális gáz entrópiája|Ideális gáz entrópiájáról szóló feladatban]] kapott entrópia-kifejezést, tegyük fel, hogy a teljes edényt kitöltő két gáz mindegyikének entrópiája úgy számítható, mintha a másik nem lenne jelen, és használjuk fel a Dalton-törvényt.}}{{Végeredmény|content=$$\Delta S = R n_1 \ln\frac{n_1+n_1}{n_1} + R n_2 \ln\frac{n_1+n_2}{n_2}$$}}</wlatex></includeonly>
 
</wlatex><includeonly><wlatex>{{Útmutatás|content=Alkalmazzuk az [[Termodinamika példák - Ideális gáz entrópiája|Ideális gáz entrópiájáról szóló feladatban]] kapott entrópia-kifejezést, tegyük fel, hogy a teljes edényt kitöltő két gáz mindegyikének entrópiája úgy számítható, mintha a másik nem lenne jelen, és használjuk fel a Dalton-törvényt.}}{{Végeredmény|content=$$\Delta S = R n_1 \ln\frac{n_1+n_1}{n_1} + R n_2 \ln\frac{n_1+n_2}{n_2}$$}}</wlatex></includeonly>
−
#* c) <wlatex>Számítsuk ki az entrópia-változást, ha a két edényben azonos gáz van!</wlatex><includeonly><wlatex>{{Útmutatás|content=A levezetésnél vegyük figyelembe, hogy a keverés utáni állapotban az egész edényben ''ugyanaz'' a gáz van. A különböző gázokra levezetett fenti összefüggésből nem kapunk helyes eredményt; ez a Gibbs-féle paradoxon.}}</wlatex><wlatex>{{Végeredmény|content=$$\Delta S=0$$}}</wlatex></includeonly><noinclude>
+
#* c) <wlatex>Számítsuk ki az entrópia-változást, ha a két edényben ''azonos fajtájú'' gáz van!</wlatex><includeonly><wlatex>{{Útmutatás|content=A levezetésnél vegyük figyelembe, hogy a keverés utáni állapotban az egész edényben ''ugyanaz'' a gáz van. A különböző gázokra levezetett fenti összefüggésből nem kapunk helyes eredményt; ez a Gibbs-féle paradoxon.}}</wlatex><wlatex>{{Végeredmény|content=$$\Delta S=0$$}}</wlatex></includeonly><noinclude>
  
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>'''a)'''A két edény paramétereit alsó indexek számokkal ($i=1,2$), a gázokat betűkkel ($j=A,B$) különböztetjük meg. Kezdetben az állapotegyenlet:
+
<wlatex>'''a)'''A két edény paramétereit alsó indexek számokkal ($i=1,2$), a gázokat betűkkel ($j=A,B$) különböztetjük meg. Kezdetben az állapotegyenletek:
−
$$ p V_1= N_1kT $$
+
$$ p V_1= N_A kT, \qquad p V_2= N_B kT. $$
−
$$ p V_2= N_2kT $$
+
 
A fal elvétele után a Dalton-törvényt felhasználva a kialakuló parciális nyomások:
 
A fal elvétele után a Dalton-törvényt felhasználva a kialakuló parciális nyomások:
−
$$ p_A=\frac{N_1kT}{V_1+ V_2}$$
+
$$ p_A=\frac{N_A kT} {V_1+ V_2}, \qquad p_B=\frac{N_B kT} {V_1+ V_2}$$
−
$$ p_B=\frac{N_2kT}{V_1+ V_2}$$
+
és a $p^*$ össznyomás
−
és a $p*$ össznyomás
+
$$ p^* = p_1+p_2 = \frac{N_A kT + N_B kT}{V_1+ V_2} = \frac{p V_1 + p V_2}{V_1+ V_2} = p. $$
−
$ p* = p_1+p_2 = \frac{N_1kT+ N_2kT}{V_1+ V_2} = p $$
+
  
−
'''b)''' Az I. főtételt kiintegrálva korábban kaptuk, hogy:
+
'''b)''' Az I. főtételt kiintegrálva [[Termodinamika példák - Az entrópia hőmérséklet- és térfogatfüggése, az adiabata egyenlete|korábban megkaptuk]] az entrópia hőmérséklet- és térfogatfüggését:
−
$$ \Delta S_j = n_j C_{Vj} \ln \frac{V_{j\text{veg}}}{V_{j\text{kezd}} +n_j R \ln \frac{V_{j\text{veg}}}{V_{j\text{kezd}} $$
+
$$ \Delta S_j = n_j C_{Vj} \ln\frac{T_{j\text{vég}}}{T_{j\text{kezd}}} +n_j R \ln\frac{V_{j\text{vég}}}{V_{j\text{kezd}}}, $$
 +
most $V_{A\text{kezd}}=V_1$, $V_{B\text{kezd}}=V_2$ és $V_{A\text{vég}}=V_{B\text{vég}}=V_1+V_2$.
  
−
Ezzel a két gáz entrópia-változásának összege:
+
Most a hőmérséklet végig állandó (az ''a)'' részben azt láttuk be, hogy a kezdeti- és a végállapotban ugyanaz, a feladat megoldásához ez is elég). Ezekkel a két gáz entrópia-változásának összege:
 +
$$ \Delta S = k\left(N_A \ln\frac{V_1+V_2}{V_1}+ N_B\ln \frac{V_1+V_2}{V_2}\right) $$
  
−
$$\Delta S=R\left( n_1\ln \frac{V_1+ V_2}{V_1}+ n_2\ln \frac{V_1+ V_2}{V_2}\right)$$
+
$$ V_1=\frac{n_A RT} p, \qquad V_2=\frac{n_B RT} p$$
 +
$$ \Delta S = R \left( n_A \ln\frac{n_A+n_B}{n_1}+ n_B \ln\frac{n_A+n_B}{n_B}\right)>0, $$
 +
ami a feladatban adott $n_A\equiv n_1$ és $n_B\equiv n_2$ értékekkel
 +
$$ \Delta S = R \left( n_1 \ln\frac{n_1+n_2}{n_1}+ n_2 \ln\frac{n_1+n_2}{n_2}\right)>0. $$
  
−
$$  V_1=\frac{n_1RT} p $$
+
'''c)''' Ha a két edényben azonos gáz van, akkor bármelyik pillanatban munkavégzés nélkül visszatehetjük a válaszfalat és ugyanúgy az ''egyensúlyi'' kezdeti makroállapotot kapjuk eredményként, az entrópia nem változhatott meg noha a ''b)'' pontban kapott eredmény ezt sugallja, ez a Gibbs-paradoxon.
  
−
$$  V_2=\frac{n_2RT} p$$ \Delta S=R\left( n_1\ln \frac{n_1+ n_2}{n_1}+ n_2\ln \frac{n_1+ n_2}{n_2}\right) $$
+
... számítás ...
  
−
c)
+
== Megjegyzés: a Gibbs-paradoxon ==
  
−
Ha azonos gáz van mindkét tartályban, akkor azt várnánk, hogy $\Delta S=0$, viszont az előbbi összeg mindkét tagja nagyobb nullánál. A Boltzmann-féle entrópiával számolva:
+
Az eltérés a klasszikus részecskeképben és az entrópia definíciójában keresendő: a végállapot entrópiájának számításakor feltettük, hogy meg tudjuk különböztetni, kezdetben melyik részecske melyik tartályban volt, ami különböző anyagi minőség esetén lehetséges is. A kvantummechanika eredményei szerint viszont az azonos anyagi minőségű részecskék ''megkülönböztethetetlenek'', azaz miután egyetlen közös térbe engedtük őket, elméletben sincs olyan mérés, ami egyszerre megmondja a kezdőfeltételeket (a részecskék pontos sebességét ''és'' pontos helyét), sem olyan, amelyik megmondja, melyik részecske eredetileg melyik tartályban volt.
  
−
Az első tartályt ''p'', a másodikat ''q'' darab cellára osztjuk fel, amelyekben rendre ''N'_1, N'_2, …, N'_p, N'_{p+1</sub>, …, N'<sub>p+q''</sub> részecske van. Ezt a makroállapotot a fal elvétele előtt ''W<sub>1}''-féle mikroállapot valósíthatja meg. Az ''N_1+N_2'' darab részecskét – mivel azok azonos fajtájúak – a két edényben rendelkezésre álló ''N_1+N_2'' helyükre $\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}$-féleképpen oszthatjuk szét. Majd ezeket az adott edényükben levő cellákban is szét kell osztanunk:
+
Ezért az entrópiadefiníciót ki kell egészítenünk a megkülönböztethetetlenséggel, azaz azonos anyagi minőségű részecskék permutációja nem vezet új makroállapothoz:
 +
$$ S^* = k \ln\frac{W}{N!} $$
  
−
$$ W_1=\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}\cdot \frac{N_1!}{\prod _{i=1}^pN{\,\mathrm '}_i!}\cdot \frac{N_2!}{\prod _{i=p+1}^{p+q}N{\,\mathrm '}_i!}=\frac{\left( N_1+ N_2\right)!}{\prod _{i=1}^{p+q}N{\,\mathrm '}_i!}$$
 
  
−
A fal felnyitását követően is osszuk fel az egybenyitott edényeket az előbbi makroállapotnak megfelelően (''N'_1, …, N'_{p+q}''). Ekkor a ''W_2'' termodinamikai valószínűség:
+
=== Megjegyzés 2 ===
  
−
$$ W_2=\frac{\left( N_1+ N_2\right)!}{\prod _{i=1}^{p+q}N{\,\mathrm '}_i!}$$
+
Találkozhatunk olyan levezetéssel, ami a tartályokat további képzeletbeli egységekre bontja, és a ''azonos fajtájú'' gázra számszerűen helyes eredményt ad. Ezt a levezetést alább közöljük, de kevésbé ajánljuk, mert nem tisztázza a megkülönböztethetetlenség kérdését, ugyanakkor a formalizmust feleslegesen bonyolítja.
 +
 
 +
<small>Legyen azonos fajtájú gáz van mindkét tartályban, a Boltzmann-féle entrópiával számolunk.
 +
Az első tartályt $p$, a másodikat $q$ darab cellára osztjuk fel, amelyekben rendre $N'_1, N'_2, \ldots, N'_p, N'_{p+1}, \ldots, N'_{p+q}$ részecske van. Ezt a makroállapotot a fal elvétele előtt $W_1$-féle mikroállapot valósíthatja meg. Az $N_1+N_2$ darab részecskét – mivel azok azonos fajtájúak – a két edényben rendelkezésre álló $N_1+N_2$ helyükre $\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}$-féleképpen oszthatjuk szét. Majd ezeket az adott edényükben levő cellákban is szét kell osztanunk:
 +
 
 +
$$ W_1=\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}\cdot \frac{N_1!}{\prod _{i=1}^pN{\,\mathrm '}_i!}\cdot \frac{N_2!}{\prod _{i=p+1}^{p+q}N{\,\mathrm '}_i!}=\frac{\left( N_1+ N_2\right)!}{\prod _{i=1}^{p+q}N{\,\mathrm '}_i!}.$$
 +
 
 +
A fal felnyitását követően is osszuk fel az egybenyitott edényeket az előbbi makroállapotnak megfelelően ($N'_1, \ldots, N'_{p+q}$). Ekkor a $W_2$ termodinamikai valószínűség:
 +
 
 +
$$ W_2=\frac{\left( N_1+ N_2\right)!}{\prod _{i=1}^{p+q}N{\,\mathrm '}_i!}.$$
  
 
Ezekkel a Boltzmann-féle entrópia:
 
Ezekkel a Boltzmann-féle entrópia:
  
−
$$\Delta S=k\ln \frac{W_2}{W_1}=0$$
+
$$\Delta S=k\ln \frac{W_2}{W_1}=0.$$
  
−
Ha kezdetben a két edényben különböző gázok volnának, akkor ''W_1''-ben az $\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}$ tag eltűnne, hiszen csak egyféleképpen tudnánk szétosztani a részecskéket a tartályok között. Ekkor:
+
Ha kezdetben a két edényben különböző gázok volnának, akkor $W_1$'-ben az $\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}$ tényező eltűnne, hiszen csak egyféleképpen tudnánk szétosztani a részecskéket a tartályok között. Ekkor:
  
−
$$\Delta S=k\ln \frac{W_2}{W_1}=k\ln \frac{\left( N_1+ N_2\right)!}{N_1! N_2!}$$
+
$$\Delta S=k\ln \frac{W_2}{W_1}=k\ln \frac{\left( N_1+ N_2\right)!}{N_1! N_2!}.$$</small>
  
−
Az $\ln N!\approx N\ln N-N$ Stirling-formulát felhasználva a b)-beli összefüggést kapjuk vissza.
+
Vegyük észre, hogy a fal felnyitása előtt és után ugyanannyi részecske volt az egyes képzeletbeli cellákban, ez csak egyensúlyban, makroszkopikusan nagy cellákra igaz. Vegyük még észre, hogy élhetünk a $p=q=1$ választással, ekkor azonos fajtájú gázra $W_1$ és $W_2$ már az egyszerűsítés előtt ugyanazt az alakot ölti, ami a gázrészecskék egymás közötti teljes felcserélhetőségére utal, ami a kezdőállapotban kvantummechanikailag nem is igaz; különböző fajtájú gázokra $W_1=1$ és $W_2=\frac{\left(N_1+ N_2\right)!}{N_1! N_2!}$, amit könnyebben magyarázhatunk a megkülönböztethetőséggel.
  
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap 2013. április 15., 21:20-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Entrópia, II. főtétel
Feladatok listája:
  1. Izoterm tágulás
  2. Izobár táguláskor
  3. S(T,V), adiabata
  4. Id. g. entrópiája
  5. Forralás
  6. Hőcsere
  7. Carnot-körfolyamat
  8. Keveredési entrópia
    Gibbs-paradoxon
  9. Kaloriméterben
  10. Entrópiaváltozások
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

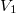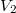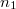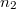  1. Egymástól válaszfallal elzárt, \setbox0\hbox{$V_1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$V_2$}% \message{//depth:\the\dp0//}% \box0% térfogatú két edényben azonos hőmérsékletű, azonos nyomású, \setbox0\hbox{$n_1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$n_2$}% \message{//depth:\the\dp0//}% \box0% mólszámú, különböző fajtájú ideális gáz van. Ha a válaszfalat eltávolítjuk, akkor a két gáz összekeveredik.
    • a) Indokoljuk meg, hogy a folyamatban miért nem változik a hőmérséklet és a nyomás!
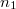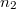    • b) Határozzuk meg az entrópia-változást (az ún. keverési entrópiát), és fejezzük ki a gázok \setbox0\hbox{$n_1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$n_2$}% \message{//depth:\the\dp0//}% \box0% mólszámaival!
    • c) Számítsuk ki az entrópia-változást, ha a két edényben azonos fajtájú gáz van!

Megoldás

a)A két edény paramétereit alsó indexek számokkal (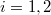\setbox0\hbox{$i=1,2$}% \message{//depth:\the\dp0//}% \box0%), a gázokat betűkkel (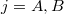\setbox0\hbox{$j=A,B$}% \message{//depth:\the\dp0//}% \box0%) különböztetjük meg. Kezdetben az állapotegyenletek:

\[ p V_1= N_A kT, \qquad p V_2= N_B kT. \]

A fal elvétele után a Dalton-törvényt felhasználva a kialakuló parciális nyomások:

\[ p_A=\frac{N_A kT} {V_1+ V_2}, \qquad p_B=\frac{N_B kT} {V_1+ V_2}\]

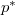és a \setbox0\hbox{$p^*$}% \message{//depth:\the\dp0//}% \box0% össznyomás

\[ p^* = p_1+p_2 = \frac{N_A kT + N_B kT}{V_1+ V_2} = \frac{p V_1 + p V_2}{V_1+ V_2} = p. \]

b) Az I. főtételt kiintegrálva korábban megkaptuk az entrópia hőmérséklet- és térfogatfüggését:

\[ \Delta S_j = n_j C_{Vj} \ln\frac{T_{j\text{vég}}}{T_{j\text{kezd}}} +n_j R \ln\frac{V_{j\text{vég}}}{V_{j\text{kezd}}}, \]

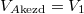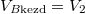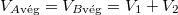most \setbox0\hbox{$V_{A\text{kezd}}=V_1$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$V_{B\text{kezd}}=V_2$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$V_{A\text{vég}}=V_{B\text{vég}}=V_1+V_2$}% \message{//depth:\the\dp0//}% \box0%.

Most a hőmérséklet végig állandó (az a) részben azt láttuk be, hogy a kezdeti- és a végállapotban ugyanaz, a feladat megoldásához ez is elég). Ezekkel a két gáz entrópia-változásának összege:

\[ \Delta S = k\left(N_A \ln\frac{V_1+V_2}{V_1}+ N_B\ln \frac{V_1+V_2}{V_2}\right) \]
\[ V_1=\frac{n_A RT} p, \qquad V_2=\frac{n_B RT} p\]
\[ \Delta S = R \left( n_A \ln\frac{n_A+n_B}{n_1}+ n_B \ln\frac{n_A+n_B}{n_B}\right)>0, \]

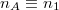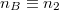ami a feladatban adott \setbox0\hbox{$n_A\equiv n_1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$n_B\equiv n_2$}% \message{//depth:\the\dp0//}% \box0% értékekkel

\[ \Delta S = R \left( n_1 \ln\frac{n_1+n_2}{n_1}+ n_2 \ln\frac{n_1+n_2}{n_2}\right)>0. \]

c) Ha a két edényben azonos gáz van, akkor bármelyik pillanatban munkavégzés nélkül visszatehetjük a válaszfalat és ugyanúgy az egyensúlyi kezdeti makroállapotot kapjuk eredményként, az entrópia nem változhatott meg noha a b) pontban kapott eredmény ezt sugallja, ez a Gibbs-paradoxon.

... számítás ...

Megjegyzés: a Gibbs-paradoxon

Az eltérés a klasszikus részecskeképben és az entrópia definíciójában keresendő: a végállapot entrópiájának számításakor feltettük, hogy meg tudjuk különböztetni, kezdetben melyik részecske melyik tartályban volt, ami különböző anyagi minőség esetén lehetséges is. A kvantummechanika eredményei szerint viszont az azonos anyagi minőségű részecskék megkülönböztethetetlenek, azaz miután egyetlen közös térbe engedtük őket, elméletben sincs olyan mérés, ami egyszerre megmondja a kezdőfeltételeket (a részecskék pontos sebességét és pontos helyét), sem olyan, amelyik megmondja, melyik részecske eredetileg melyik tartályban volt.

Ezért az entrópiadefiníciót ki kell egészítenünk a megkülönböztethetetlenséggel, azaz azonos anyagi minőségű részecskék permutációja nem vezet új makroállapothoz:

\[ S^* = k \ln\frac{W}{N!} \]


Megjegyzés 2

Találkozhatunk olyan levezetéssel, ami a tartályokat további képzeletbeli egységekre bontja, és a azonos fajtájú gázra számszerűen helyes eredményt ad. Ezt a levezetést alább közöljük, de kevésbé ajánljuk, mert nem tisztázza a megkülönböztethetetlenség kérdését, ugyanakkor a formalizmust feleslegesen bonyolítja.

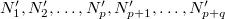Legyen azonos fajtájú gáz van mindkét tartályban, a Boltzmann-féle entrópiával számolunk. Az első tartályt \setbox0\hbox{$p$}% \message{//depth:\the\dp0//}% \box0%, a másodikat \setbox0\hbox{$q$}% \message{//depth:\the\dp0//}% \box0% darab cellára osztjuk fel, amelyekben rendre \setbox0\hbox{$N'_1, N'_2, \ldots, N'_p, N'_{p+1}, \ldots, N'_{p+q}$}% \message{//depth:\the\dp0//}% \box0% részecske van. Ezt a makroállapotot a fal elvétele előtt 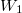\setbox0\hbox{$W_1$}% \message{//depth:\the\dp0//}% \box0%-féle mikroállapot valósíthatja meg. Az 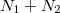\setbox0\hbox{$N_1+N_2$}% \message{//depth:\the\dp0//}% \box0% darab részecskét – mivel azok azonos fajtájúak – a két edényben rendelkezésre álló 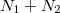\setbox0\hbox{$N_1+N_2$}% \message{//depth:\the\dp0//}% \box0% helyükre 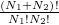\setbox0\hbox{$\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}$}% \message{//depth:\the\dp0//}% \box0%-féleképpen oszthatjuk szét. Majd ezeket az adott edényükben levő cellákban is szét kell osztanunk:

\[ W_1=\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}\cdot \frac{N_1!}{\prod _{i=1}^pN{\,\mathrm '}_i!}\cdot \frac{N_2!}{\prod _{i=p+1}^{p+q}N{\,\mathrm '}_i!}=\frac{\left( N_1+ N_2\right)!}{\prod _{i=1}^{p+q}N{\,\mathrm '}_i!}.\]

A fal felnyitását követően is osszuk fel az egybenyitott edényeket az előbbi makroállapotnak megfelelően (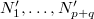\setbox0\hbox{$N'_1, \ldots, N'_{p+q}$}% \message{//depth:\the\dp0//}% \box0%). Ekkor a 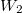\setbox0\hbox{$W_2$}% \message{//depth:\the\dp0//}% \box0% termodinamikai valószínűség:

\[ W_2=\frac{\left( N_1+ N_2\right)!}{\prod _{i=1}^{p+q}N{\,\mathrm '}_i!}.\]

Ezekkel a Boltzmann-féle entrópia:

\[\Delta S=k\ln \frac{W_2}{W_1}=0.\]

Ha kezdetben a két edényben különböző gázok volnának, akkor 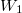\setbox0\hbox{$W_1$}% \message{//depth:\the\dp0//}% \box0%'-ben az 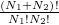\setbox0\hbox{$\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}$}% \message{//depth:\the\dp0//}% \box0% tényező eltűnne, hiszen csak egyféleképpen tudnánk szétosztani a részecskéket a tartályok között. Ekkor:

\[\Delta S=k\ln \frac{W_2}{W_1}=k\ln \frac{\left( N_1+ N_2\right)!}{N_1! N_2!}.\]

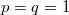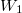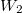Vegyük észre, hogy a fal felnyitása előtt és után ugyanannyi részecske volt az egyes képzeletbeli cellákban, ez csak egyensúlyban, makroszkopikusan nagy cellákra igaz. Vegyük még észre, hogy élhetünk a \setbox0\hbox{$p=q=1$}% \message{//depth:\the\dp0//}% \box0% választással, ekkor azonos fajtájú gázra \setbox0\hbox{$W_1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$W_2$}% \message{//depth:\the\dp0//}% \box0% már az egyszerűsítés előtt ugyanazt az alakot ölti, ami a gázrészecskék egymás közötti teljes felcserélhetőségére utal, ami a kezdőállapotban kvantummechanikailag nem is igaz; különböző fajtájú gázokra 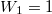\setbox0\hbox{$W_1=1$}% \message{//depth:\the\dp0//}% \box0% és \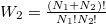setbox0\hbox{$W_2=\frac{\left(N_1+ N_2\right)!}{N_1! N_2!}$}% \message{//depth:\the\dp0//}% \box0%, amit könnyebben magyarázhatunk a megkülönböztethetőséggel.


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Termodinamika_példák_-_Keveredési_entrópia,_Gibbs-paradoxon&oldid=8877”