Termodinamika példák - Keveredési entrópia, Gibbs-paradoxon

Feladat

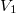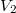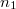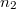1. Egymástól válaszfallal elzárt, $\setbox0\hbox{$V_1$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$V_2$}% \message{//depth:\the\dp0//}% \box0%$ térfogatú két edényben azonos hőmérsékletű, azonos nyomású, $\setbox0\hbox{$n_1$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$n_2$}% \message{//depth:\the\dp0//}% \box0%$ mólszámú, különböző fajtájú ideális gáz van. Ha a válaszfalat eltávolítjuk, akkor a két gáz összekeveredik.
   • a) Indokoljuk meg, hogy a folyamatban miért nem változik a hőmérséklet és a nyomás!
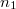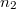   • b) Határozzuk meg az entrópia-változást (az ún. keverési entrópiát), és fejezzük ki a gázok $\setbox0\hbox{$n_1$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$n_2$}% \message{//depth:\the\dp0//}% \box0%$ mólszámaival!
   • c) Számítsuk ki az entrópia-változást, ha a két edényben azonos gáz van!

Megoldás

a)A két edény paramétereit alsó indexek számokkal (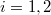$\setbox0\hbox{$i=1,2$}% \message{//depth:\the\dp0//}% \box0%$), a gázokat betűkkel (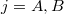$\setbox0\hbox{$j=A,B$}% \message{//depth:\the\dp0//}% \box0%$) különböztetjük meg. Kezdetben az állapotegyenlet:

$\[ p V_1= N_1kT \]$

$\[ p V_2= N_2kT \]$

A fal elvétele után a Dalton-törvényt felhasználva a kialakuló parciális nyomások:

$\[ p_A=\frac{N_1kT}{V_1+ V_2}\]$

$\[ p_B=\frac{N_2kT}{V_1+ V_2}\]$

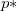és a $\setbox0\hbox{$p*$}% \message{//depth:\the\dp0//}% \box0%$ össznyomás

$ p* = p_1+p_2 = \frac{N_1kT+ N_2kT}{V_1+ V_2} = p

$\[\]$

b) Az I. főtételt kiintegrálva korábban kaptuk, hogy:

\[ \Delta S_j = n_j C_{Vj} \ln \frac{V_{j\text{veg}}}{V_{j\text{kezd}} +n_j R \ln \frac{V_{j\text{veg}}}{V_{j\text{kezd}} \]

Ezzel a két gáz entrópia-változásának összege:

$\[\Delta S=R\left( n_1\ln \frac{V_1+ V_2}{V_1}+ n_2\ln \frac{V_1+ V_2}{V_2}\right)\]$

$\[ V_1=\frac{n_1RT} p \]$

$\[ V_2=\frac{n_2RT} p\]$

\Delta S=R\left( n_1\ln \frac{n_1+ n_2}{n_1}+ n_2\ln \frac{n_1+ n_2}{n_2}\right)

$\[\]$

c)

Ha azonos gáz van mindkét tartályban, akkor azt várnánk, hogy 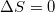$\setbox0\hbox{$\Delta S=0$}% \message{//depth:\the\dp0//}% \box0%$, viszont az előbbi összeg mindkét tagja nagyobb nullánál. A Boltzmann-féle entrópiával számolva:

Az első tartályt p, a másodikat q darab cellára osztjuk fel, amelyekben rendre N'_1, N'_2, …, N'_p, N'_{p+1</sub>, …, N'_p+q részecske van. Ezt a makroállapotot a fal elvétele előtt W_1}-féle mikroállapot valósíthatja meg. Az N_1+N_2 darab részecskét – mivel azok azonos fajtájúak – a két edényben rendelkezésre álló N_1+N_2 helyükre 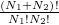$\setbox0\hbox{$\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}$}% \message{//depth:\the\dp0//}% \box0%$-féleképpen oszthatjuk szét. Majd ezeket az adott edényükben levő cellákban is szét kell osztanunk:

$\[ W_1=\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}\cdot \frac{N_1!}{\prod _{i=1}^pN{\,\mathrm '}_i!}\cdot \frac{N_2!}{\prod _{i=p+1}^{p+q}N{\,\mathrm '}_i!}=\frac{\left( N_1+ N_2\right)!}{\prod _{i=1}^{p+q}N{\,\mathrm '}_i!}\]$

A fal felnyitását követően is osszuk fel az egybenyitott edényeket az előbbi makroállapotnak megfelelően (N'_1, …, N'_{p+q}). Ekkor a W_2 termodinamikai valószínűség:

$\[ W_2=\frac{\left( N_1+ N_2\right)!}{\prod _{i=1}^{p+q}N{\,\mathrm '}_i!}\]$

Ezekkel a Boltzmann-féle entrópia:

$\[\Delta S=k\ln \frac{W_2}{W_1}=0\]$

Ha kezdetben a két edényben különböző gázok volnának, akkor W_1-ben az 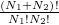$\setbox0\hbox{$\frac{\left( N_1+ N_2\right)!}{N_1! N_2!}$}% \message{//depth:\the\dp0//}% \box0%$ tag eltűnne, hiszen csak egyféleképpen tudnánk szétosztani a részecskéket a tartályok között. Ekkor:

$\[\Delta S=k\ln \frac{W_2}{W_1}=k\ln \frac{\left( N_1+ N_2\right)!}{N_1! N_2!}\]$

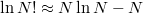Az $\setbox0\hbox{$\ln N!\approx N\ln N-N$}% \message{//depth:\the\dp0//}% \box0%$ Stirling-formulát felhasználva a b)-beli összefüggést kapjuk vissza.