Magnetosztatika példák - Áram által átjárt üreges hengerben a mágneses tér
Feladat
- Tömör fémből készült, hosszú, egyenes körhengerben ugyancsak henger alakú üreget készítünk. Az üreg tengelye
 távolságra van a henger tengelyétől. Az üreges hengerben egyenletes
távolságra van a henger tengelyétől. Az üreges hengerben egyenletes  áramsűrűséggel tengelyirányú áram folyik. Milyen a mágneses térerősség az üreg belsejében?
áramsűrűséggel tengelyirányú áram folyik. Milyen a mágneses térerősség az üreg belsejében?
Megoldás
Alkalmazzuk a szuperpozíció elvét! Az üreges hengerben folyó áramot elképzelhetjük úgy, mintha egy tömör hengerben folyna áram homogén  áramsűrűséggel, melyhez hozzáadjuk egy kisebb vezető henger ugyancsak homogén,
áramsűrűséggel, melyhez hozzáadjuk egy kisebb vezető henger ugyancsak homogén, 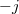 áramsűrűség eloszlását. Az árameloszlás két összetevője által keltett mágneses terek szuperpozíciója megegyezik az üreges hengerben folyó áram mágneses terével. A homogén,
áramsűrűség eloszlását. Az árameloszlás két összetevője által keltett mágneses terek szuperpozíciója megegyezik az üreges hengerben folyó áram mágneses terével. A homogén,  áramsűrűséggel átjárt henger belsejében ismerjük a teret az Áram által átjárt hengeres vezetékben a mágneses tér feladatából:
áramsűrűséggel átjárt henger belsejében ismerjük a teret az Áram által átjárt hengeres vezetékben a mágneses tér feladatából:
![\[\vec{H}=\dfrac{\vec{j}\times \vec{r}}{2}\]](/images/math/d/8/2/d823d23573ad252f1a1b83c7b208cbc8.png)
Mi most egy  és egy
és egy 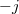 árammal átjárt henger
árammal átjárt henger 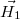 és
és 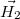 terét határozzuk meg:
terét határozzuk meg:
![\[\vec{H_1}=\dfrac{\vec{j}\times \vec{r}}{2}\]](/images/math/f/7/f/f7f37977a4761e89141bdc7383232a58.png)
![\[\vec{H_2}=-\dfrac{\vec{j}\times \vec{r'}}{2}\]](/images/math/1/b/9/1b942b0ccb558e634455298f74ac5ee4.png)
Ahol 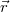 az első,
az első, 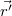 pedig a második henger tengelyétől a vizsgált pontba mutató vektor. Mivel a hengerek tengelyei egymástól
pedig a második henger tengelyétől a vizsgált pontba mutató vektor. Mivel a hengerek tengelyei egymástól 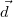 távolságra helyezkednek el,
távolságra helyezkednek el, 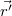 kifejezhető a következőképpen:
kifejezhető a következőképpen:
![\[\vec{r'}=\vec{r}-\vec{d}\]](/images/math/3/e/2/3e25090fbebf66b4b78e6deb88cd922f.png)
Ez alapján 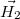 a következő:
a következő:
![\[\vec{H_2}=-\dfrac{\vec{j}\times \vec{r'}}{2}=-\dfrac{\vec{j}\times \left( \vec{r}-\vec{d} \right) }{2}=\dfrac{\vec{j}\times \vec{d}}{2}-\dfrac{\vec{j}\times \vec{r}}{2}\]](/images/math/8/1/3/8139b0985b370cb0d1939aa08fed110e.png)
A két henger terének szuperpozíciója megadja a lyukas henger üregében mérhető teret:
![\[\vec{H}=\vec{H_1}+\vec{H_2}=\dfrac{\vec{j}\times \vec{r}}{2}+\dfrac{\vec{j}\times \vec{d}}{2}-\dfrac{\vec{j}\times \vec{r}}{2}=\dfrac{\vec{j}\times \vec{d}}{2}\]](/images/math/8/7/a/87a35b805674d78e5eaf8ac61782d474.png)
A megoldás meglepő: Az üregben mérhető tér homogén, nagysága csak henger és az üreg tengelytávolságától függ.