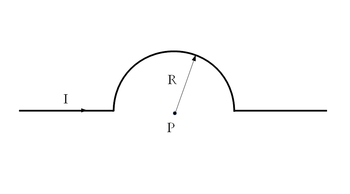
Magnetosztatika példák - Áram által átjárt vezető elrendezés mágneses tere
Feladat
- Határozzuk meg a mágneses indukciót az ábra alapján megadott
áram által átjárt vezető elrendezés 
pontjában!(ábra) 
Megoldás
Mivel a rendszer nem rendelkezik olyan szimmetriákkal, amelyek az Amper-féle gerjesztési törvény alkalmazását egyszerűvé tennék, a mágneses indukció meghatározásához a Biot-Savart törvényt használjuk:
![\[B=\frac{\mu_0 I}{4 \pi} \int \frac{\vec{dl}\times \vec{r}}{\mid \vec{r} \mid ^3}\]](/images/math/3/e/9/3e9a20b8689b5013babc48b359a638d8.png)
Az ábra alapján beláthatjuk, hogy a két egyenes vezetőszakasz tengelye átmegy a ponton, így ezen vezetőszakaszokon a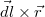 
vektorszorzat azonosan nullát ad. Ez azt jelenti, hogy a pontban mágneses teret csak a fékörív kelt. Vegyük a körív egy 
hosszúságú infinitezimális ívelemét, mely a középpontból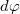 
szög alatt látszik. Az ívdarab hossza:
![\[dl=Rd\varphi\]](/images/math/3/1/a/31a804f711a1b070a6143e68d4d7c0e5.png)
Bármely tetszőlegesen kiválasztott ívelem 
távolságra van a ponttól, továbbá megállapítható, hogy az ívelemek mindig merőlegesek a középpontból feléjük húzott 
sugárra. A Biot-Savart törvényben található 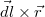vektorszorzat tehát mindig merőleges a körív síkjára, nagysága pedig felírható a mennyiségek skalárértékeinek szorzataként:
![\[B=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{dlR}{ R^3}=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{dl}{ R^2}=\dfrac{\mu_0 I}{4 \pi} \int_0^{\pi} \dfrac{d\varphi}{ R}\]](/images/math/0/a/1/0a1607d97b22b0d3aa57ffa04d42013a.png)
Az integrál kiszámítása után a mágneses indukció:
![\[B=\dfrac{\mu_0 I}{4 \pi R} \pi=\dfrac{\mu_0 I}{4 R}\]](/images/math/d/5/3/d53dd483c5b0ce1e917e9632b9c80c50.png)
