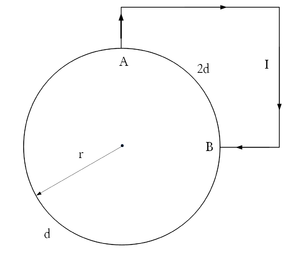
Magnetosztatika példák - Körív alakú vezető mágneses tere
Feladat
- Az ábrán látható vezető körben
áram folyik.
a) Mekkora és milyen irányú az
sugarú kör középpontjában a mágneses térerősségnek a körvezetőtől származó része, ha az 
és 
pontokat összekötő negyedkörív alakú vezető keresztmetszete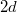 
átmérőjű, míg a háromnegyed körívé 
?
b) Mekkora és milyen irányú mágneses teret kelt a körhöz csatlakozó két vezető szakasz?
c) Mekkora és milyen irányú teret kelt a másik két egyenes vezető szakasz, ha ezeknek a szakaszoknak a hossza
?
d) Mekkora és milyen irányú a teljes rendszer által létrehozott mágneses tér a kör középpontjában?
Megoldás
a.) A feladat megoldásának gondolatmenete hasonló a Gyűrű alakú vezető mágneses tere feladatához. Először tehát meghatározzuk az egyes körívek ellenállását. Legyen a vezető fajlagos ellenállása 
![\[R_1=\rho\dfrac{l_1}{A_1}=\rho\dfrac{\dfrac{1}{4}2r\pi}{\dfrac{(2d)^2}{4}\pi}=\dfrac{\rho r}{2d^2}\]](/images/math/a/8/e/a8e70a1a2a569c2d86288b5881b8215e.png)
![\[R_2=\rho\dfrac{l_2}{A_2}=\rho\dfrac{\dfrac{3}{4}2r\pi}{\dfrac{d^2}{4}\pi}=\dfrac{6\rho r}{d^2}\]](/images/math/6/3/0/6304ad85fdafb48e49adad70402eb9f8.png)
A két ellenállás hányadosa:
![\[\dfrac{R_2}{R_1}=\dfrac{6\rho r}{d^2}\dfrac{2d^2}{\rho r}=12\]](/images/math/e/2/7/e27ca815a5c4acfad28e469ee1569fe6.png)
Mivel az és pontok között a két vezető körív párhuzamosan van kapcsolva, a főkörben folyó áram a körívek ellenállásával fordított arányban oszlik meg a két ív között:
![\[I_1=I\dfrac{R_2}{R_1+R_2}=I\dfrac{12R_1}{R_1+12R_1}=\dfrac{12}{13}I\]](/images/math/1/6/6/16677bb096aa84e1b4663b123c42f227.png)
![\[I_2=-I\dfrac{R_1}{R_1+R_2}=-I\dfrac{R_1}{R_1+12R_1}=-\dfrac{1}{13}I\]](/images/math/e/c/a/ecae2fe9db0c20e8a14c96b44957e8b5.png)
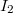azért kapott negatív előjelet, mert a háromnegyed körívben az áram körüljárási iránya ellentétes a negyedkörívben folyó áraméval.
A Gyűrű alakú vezető mágneses tere feladatában már meghatároztuk az sugarú, áram által átjárt 
szögű körív mágneses terét a Biot-Savart törvény segítségével:
![\[B=\dfrac{\mu_0 I}{4 \pi r}\alpha\]](/images/math/b/1/2/b125eeb8e22acc8c9da3ae958b5dc525.png)
Az így kapott mágneses indukció iránya merőleges a körív síkjára. A pozitív irány az ábra síkjából kifelé mutat. A negyed, és a háromnegyed körív által keltett terek tehát a következők:
![\[B_1=\dfrac{\mu_0 I_1}{4 \pi r}\dfrac{\pi}{2}=\dfrac{3\mu_0 I}{26 r}\]](/images/math/f/e/1/fe1cd18b1dc4fdbc28a093ed6dc6030f.png)
![\[B_2=\dfrac{\mu_0 I_2}{4 \pi r}\dfrac{3\pi}{2}=-\dfrac{3\mu_0 I}{104 r}\]](/images/math/e/c/9/ec9e2c30c3f8a20ac427b25838893f15.png)
A körívekben folyó áramok által keltett tér tehát:
![\[B_{kor}=B_1+B_2=\dfrac{3\mu_0 I}{r}\left( \dfrac{1}{26}-\dfrac{1}{104} \right)=\dfrac{9\mu_0 I}{104r}\]](/images/math/9/0/d/90dbd04a6d8e8eaebfe7fb5f2f5e2fdf.png)
b.) Mivel a körhöz csatlakozó két egyenes vezető szakaszra fektetett egyenesek átmennek a kör középpontján, a Biot-Savart törvény alapján belátható, hogy az ezen vezetékekben folyó áramok nem keltenek teret a kör középpontjában.
c.) A két hosszúságú egyenes vezető darab terét az Egyenes vezető mágneses tere feladatában szereplő véges hosszúságú áramjárta egyenes vezető terére vonatkozó összefüggéssel fogjuk meghatározni, melyet a Biot-Savart törvény kiintegrálásával kaptunk meg:
![\[B=\dfrac{\mu_0 I}{4 \pi t} (\sin(\alpha_1)-\sin(\alpha_2))\]](/images/math/d/9/2/d92576e66b717790614891fc128109bb.png)
Ahol 
a vizsgált pont és a vezetődarab távolsága,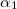 
és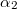 
pedig a rúd két végpontjának látószöge a vizsgált pontból a vezetékhez húzott merőlegeshez képest.
Nézzük először a 'felső', 3. jelű vezető szakaszt, melyben az áram az ábra szerint balról jobbra folyik. Ennek távolsága a kör középpontjától épp , tehát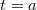 
. Mivel a vezeték hossza is , ezért a vezeték kör középpontjától távolabb eső végpontja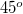 
, azaz 
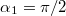radián alatt látszik. A vezető közelebbi vége pedig épp egybe esik a kör középpontjából a vezető szakaszra állított merőleges talppontjával, ezért 
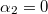Így a szóban forgó vezető szakasz által keltett 
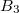mágneses tér nagysága a kör középpontjában könnyen meghatározható:
![\[B_3=-\dfrac{\mu_0 I}{4 \pi a} (\sin(\pi/2)-\sin(0))=-\dfrac{\sqrt{2} \mu_0 I}{8 \pi a}\]](/images/math/b/0/c/b0cf42fc24905224118c9eb193b26d34.png)
Az indukció nagysága azért kapott negatív előjelet, mert a Biot-Savart törvényben szereplő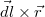 
vektoriális szorzatról belátható, hogy a fenti esetben az ábra síkjára merőleges, befelé mutató mágneses teret eredményez. Mivel korábban az ábra síkjából kifelé mutató teret definiáltuk pozitívnak, 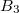előjelét negatívnak kell tekintenünk.\
Az ábrán szereplő másik hosszúságú, 4. jelű vezető szakasz mágneses terét a 3. számúhoz hasonlóan határozhatjuk meg. A vezető kör középpontjától mért távolsága szintén , látószöge szintén 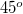, a keltett tér irányáról pedig belátható, hogy az ábra síkjára merőlegesen befelé mutat. Tehát:
![\[B_4=B_3\]](/images/math/4/d/6/4d69d670553c60280c126335bf9e4f0e.png)
A két szakasz eredő tere tehát:
![\[B_{negyzet}=2B_3=-\dfrac{\sqrt{2} \mu_0 I}{4 \pi a}\]](/images/math/5/d/3/5d345b02b632185e930ab8a19b8043b7.png)
d.) A teljes rendszer mágneses tere tehát a középpontban:
![\[B_e=B_{kor}+B_{negyzet}=\dfrac{9\mu_0 I}{104r}-\dfrac{\sqrt{2} \mu_0 I}{4 \pi a}\]](/images/math/6/6/c/66c6bda7330c9cddd6ff31000925576a.png)
