Magnetosztatika példák - Áram által átjárt hengeres vezetékben a mágneses tér

Feladat

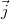1. $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú hengeres vezetékben az áramsűrűség $\setbox0\hbox{$\vec{j}$}% \message{//depth:\the\dp0//}% \box0%$ vektora mindenütt azonos és párhuzamos a henger tengelyével. A tengelyre merőleges 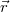$\setbox0\hbox{$\vec{r}$}% \message{//depth:\the\dp0//}% \box0%$ vektor segítségével fejezzük ki a 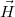$\setbox0\hbox{$\vec{H}$}% \message{//depth:\the\dp0//}% \box0%$ térerősséget az 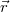$\setbox0\hbox{$\vec{r}$}% \message{//depth:\the\dp0//}% \box0%$-el jelzett pontban
   a) a hengeren belül;
   b) és kívül.

Megoldás

Szimmetria okokból feltételezhetjük, hogy a mágneses tér hengerszimmetrikus, örvényes elrendezésű lesz, nagysága egyedül a tengelytől mért távolságtól függ, iránya pedig tangenciális, azaz

$\[\vec{e}=\dfrac{\vec{j}\times \vec{r}}{jr}\]$

egységvektor irányába mutató.

a.) A tér a henger belsejében.

Felveszünk egy 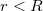$\setbox0\hbox{$r<R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú gyűrűt, melynek síkja merőleges a vezetőre, középpontja pedig egybeesik annak tengelyével. A gyűrűre, mint zárt görbére felírjuk az Amper-féle gerjesztési törvényt:

$\[I=\oint \vec{H}\vec{dl}\]$

A zárt görbe által határolt területen átfolyó $\setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0%$ áramerősség arányos a gyűrű területével, hiszen az áramsűrűség homogén:

$\[I=jA=jr^2 \pi=\oint \vec{H}\vec{dl}\]$

Mivel a rendszer hengerszimmetrikus, és tengelye irányában transzlációs szimmetriát mutat, ezért 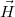$\setbox0\hbox{$\vec{H}$}% \message{//depth:\the\dp0//}% \box0%$ mindig párhuzamosd 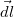$\setbox0\hbox{$\vec{dl}$}% \message{//depth:\the\dp0//}% \box0%$-el. Továbbá $\setbox0\hbox{$H$}% \message{//depth:\the\dp0//}% \box0%$ nagysága mindenütt ugyanakkora a gyűrű mentén, ezért a gerjesztési törvény egyszerűsíthető:

$\[jr^2 \pi=\oint \vec{H}\vec{dl}=\oint Hdl=2r\pi H\]$

Ebből kifejezhető a mágneses térerősség nagysága:

$\[H=\dfrac{jr}{2}\]$

A térerősség vektora pedig a következő:

$\[\vec{H}=H\vec{e}=\dfrac{jr}{2}\dfrac{\vec{j}\times \vec{r}}{jr}=\dfrac{\vec{j}\times \vec{r}}{2}\]$

b.) A tér a hengeren kívül.

Az Amper-féle gerjesztési törvényt felírhatjuk a hengeren kívüli térben felvett 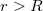$\setbox0\hbox{$r>R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú gyűrűre is. Itt azonban a zárt görbe által határolt területen átfolyó áram nagysága független a gyűrű $\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%$ sugarától:

$\[I=jR^2 \pi\]$

Így tehát a gerjesztési törvény:

$\[jR^2 \pi =2r\pi H\]$

Ebből kifejezve a térerősség nagyságát:

$\[H=\dfrac{jR^2}{2r}\]$

A térerősség vektora pedig a következő:

$\[\vec{H}=H\vec{e}=\dfrac{jR^2}{2r}\dfrac{\vec{j}\times \vec{r}}{jr}=\dfrac{R^2}{2r^2} \left(\vec{j}\times \vec{r}\right)\]$