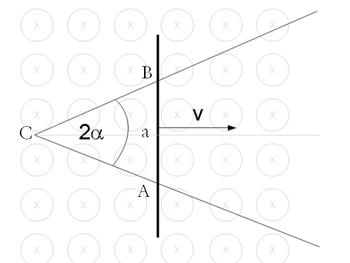
Magnetosztatika példák - V alakú sínen mozgó vezetőben indukált áram
A Fizipedia wikiből
Feladat
- Hosszegységenként
 ellenállású vezetéket úgy hajlítunk meg, hogy az ábrán látható módon
ellenállású vezetéket úgy hajlítunk meg, hogy az ábrán látható módon 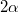 szöget alkosson. Egy könnyen csúszó rudat helyezünk az így kialakított sínre úgy, hogy ABC egyenlőszárú háromszöget alkot. A rúd ugyanabból a vezetőből készült, mint a sín. Az elrendezést a síkjára merőleges, homogén
szöget alkosson. Egy könnyen csúszó rudat helyezünk az így kialakított sínre úgy, hogy ABC egyenlőszárú háromszöget alkot. A rúd ugyanabból a vezetőből készült, mint a sín. Az elrendezést a síkjára merőleges, homogén  indukciójú térbe helyezzük. Mekkora áram folyik a hurokban, amikor a rúd
indukciójú térbe helyezzük. Mekkora áram folyik a hurokban, amikor a rúd  sebességgel mozog? (A kontaktusoknál fellépő ellenállásoktól tekintsünk el.)
sebességgel mozog? (A kontaktusoknál fellépő ellenállásoktól tekintsünk el.)
Megoldás
Geometriai megfontolások alapján az egyenlő szárú háromszög alapjának  hossza:
hossza:
![\[a = 2m\cdot\tan(\alpha)\]](/images/math/c/d/5/cd5727751c2809cb5886ab1ae41a5294.png)
ahol  a rúd távolsága a C ponttól. Ezzel a háromszög területe:
a rúd távolsága a C ponttól. Ezzel a háromszög területe:
![\[A = m^2\cdot\tan(\alpha) =v^2 t^2\cdot\tan(\alpha) \]](/images/math/2/3/7/23701ad979e5f1bcb4fad0b028babe8d.png)
Mivel a rúd egyenletes  sebességgel halad, (
sebességgel halad, (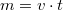 )
a keretben indukált feszültség értéke:
)
a keretben indukált feszültség értéke:
![\[U = -\frac{\partial \Phi}{\partial t} = -2 B v^2 t \cdot \tan(\alpha)\]](/images/math/a/0/2/a029cee6035eb0f251d01982af188496.png)
A vezeték ellenállása pedig:
![\[R = r\cdot l\]](/images/math/7/1/3/7132dcb660775edd6244d6cf5d37ede6.png)
ahol  a vezető keret pillanatnyi kerülete.
a vezető keret pillanatnyi kerülete.
![\[l = 2 m \left(\frac{1}{\cos(\alpha)}+\tan(\alpha)\right)\]](/images/math/5/f/6/5f66a6c1ba0e2f7f17bb57507db6a5b3.png)
A vezetőkeretben folyó áram pedig meghatározható az Ohm-törvény alapján:
![\[I = \frac{U}{R} =-\frac{ 2 B v^2 t \cdot \tan(\alpha) } {2 v t r \left(\frac{1}{\cos(\alpha)}+\tan(\alpha)\right)} = -\frac{B v \sin(\alpha)}{r \left(1+\sin(\alpha)\right)}\]](/images/math/c/9/1/c91ee547cd486734c5b4f18c9987abbb.png)