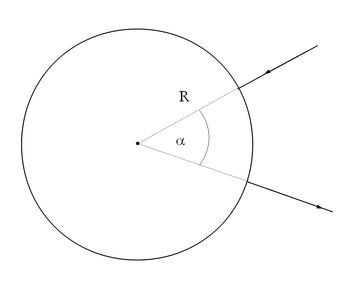
Magnetosztatika példák - Gyűrű alakú vezető mágneses tere
Feladat
- Az ábra szerinti áramkör egy homogén vezető gyűrűből áll, amelyhez két sugárirányú vezeték csatlakozik. Az áramkört záró forrás a hozzávezetésekkel együtt olyan távoli, hogy a gyűrű helyén keltett mágneses tere elhanyagolható. Mekkora a mágneses térerősség a gyűrű középpontjában?
Megoldás
Ha az  sugarú gyűrű
sugarú gyűrű  szög alatt látszódó kapcsaira
szög alatt látszódó kapcsaira  feszültséget kötünk, a kapcsok által kettéosztott ívdarab egyikében óramutató járásával megegyező, a másikban pedig óramutató járásával ellentétes áram indul. Először meghatározzuk az egyes ívelemek ellenállását, majd a bennük folyó áramot. Legvégül Biot-Savart törvénnyel kiszámítjuk az indukált mágneses teret.
feszültséget kötünk, a kapcsok által kettéosztott ívdarab egyikében óramutató járásával megegyező, a másikban pedig óramutató járásával ellentétes áram indul. Először meghatározzuk az egyes ívelemek ellenállását, majd a bennük folyó áramot. Legvégül Biot-Savart törvénnyel kiszámítjuk az indukált mágneses teret.
Az ívek hossza:
![\[L_1=\alpha r\]](/images/math/2/4/9/24906a88de613fe0357d18c71d932e51.png)
![\[L_2=(2\pi-\alpha) r\]](/images/math/5/d/4/5d463bcb462cb98d6294fb2b65e4b6f3.png)
Legyen a vezeték egységnyi hosszára eső ellenállás nagysága  . Ekkor a két ív ellenállása:
. Ekkor a két ív ellenállása:
![\[R_1=L_1\rho=\alpha r\rho\]](/images/math/5/4/e/54e1744ade6429357c559ef1b56293b8.png)
![\[R_2=(2\pi-\alpha) r\rho\]](/images/math/5/c/4/5c4d767f0b6df3e674331eb03cdbb0aa.png)
A egyes vezetékekben folyó áramok:
![\[I_1=\dfrac{U}{R_1}=\dfrac{U}{\alpha r\rho}\]](/images/math/1/0/9/1092e6408be3cb993f841012c9c4c933.png)
![\[I_2=\dfrac{U}{R_2}=\dfrac{U}{(2\pi-\alpha) r\rho}\]](/images/math/2/b/8/2b89bea7c9e5542e130eb4b54fb1e568.png)
Az áramjárta vezetők mágneses terét a kör középpontjában a Biot-Savart törvénnyel határozhatjuk meg:
![\[B=\frac{\mu_0 I}{4 \pi} \int \frac{\vec{dl} \times \vec{r}}{\vec{r}^3}\]](/images/math/f/e/b/feb44ef318f7bb852613be043461085c.png)
A vektorszorzatot egyszerűsíthetjük, hiszen az ívelemek mindig merőlegesek a hozzájuk húzott sugárra:
![\[B=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{dl r}{r^3}=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{dl }{r^2}\]](/images/math/d/0/e/d0e62b3a649c71633cb3bc5eb513ec3a.png)
Parametrizáljuk a  ívelemet a középponti szög szerint szerint mindkét ív esetén:
ívelemet a középponti szög szerint szerint mindkét ív esetén:
![\[dl_1=-r d\varphi\]](/images/math/6/3/5/635d954b4d49c736e793351fb011782d.png)
![\[dl_2=r d\varphi\]](/images/math/2/f/3/2f3077d6b5477c0b03d21a346ea889bc.png)
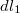 -ben azért van negatív előjel, mert az áram folyási iránya ellentétes az
-ben azért van negatív előjel, mert az áram folyási iránya ellentétes az  szög körüljárási irányával. Ezek alapján a két ív által keltett mágneses tér:
szög körüljárási irányával. Ezek alapján a két ív által keltett mágneses tér:
![\[B_1=\dfrac{\mu_0 I_1}{4 \pi} \int_0^{\alpha} \dfrac{-r d\alpha}{r^2}=-\dfrac{\mu_0 I_1}{4 \pi r} \int_0^{\alpha} d\varphi\]](/images/math/5/5/3/5536681ddd1e05967d54e9796e75031f.png)
![\[B_2=\dfrac{\mu_0 I_2}{4 \pi} \int_{\alpha}^{2\pi} \dfrac{r d\alpha}{r^2}=\dfrac{\mu_0 I_2}{4 \pi r} \int_{\alpha}^{2\pi} d\varphi\]](/images/math/f/6/b/f6b7b30e1bd47e028f4dbbd292da2c87.png)
Az integrálásokat elvégezve:
![\[B_1=-\dfrac{\mu_0 I_1}{4 \pi r} \alpha\]](/images/math/9/3/d/93d8198c745f4996d14e93b79b02e898.png)
![\[B_2=\dfrac{\mu_0 I_2}{4 \pi r} ( 2\pi-\alpha)\]](/images/math/4/a/5/4a54daca0104fee6519a4124de9a941a.png)
Behelyettesítve az áramerősségeket:
![\[B_1=-\dfrac{\mu_0 }{4 \pi r} \dfrac{U}{\alpha r\rho} \alpha=-\dfrac{\mu_0 U}{4 \pi r^2 \rho}\]](/images/math/0/9/4/094710c8993d1cff7dc207969489f919.png)
![\[B_2=\dfrac{\mu_0 I_2}{4 \pi r} \dfrac{U}{(2\pi-\alpha) r\rho}( 2\pi-\alpha)=\dfrac{\mu_0 U}{4 \pi r^2 \rho}\]](/images/math/b/4/e/b4e30ec8dd296a5d8172e407bd9f1912.png)
Az eredő mágneses indukció:
![\[B=B_1+B_2=\dfrac{\mu_0 U}{4 \pi r^2 \rho}-\dfrac{\mu_0 U}{4 \pi r^2 \rho}=0\]](/images/math/3/7/7/377287a0710ddcb6970511e35a949cdc.png)
A két komponens épp kioltja egymást, függetlenül a kontaktusok elhelyezésének  szögétől.
szögétől.
Mivel a gyűrűt vákuum tölti ki, ezért a gyűrű középpontjában a mágneses térerősség zérus.