Termodinamika példák - Van der Waals-gáz fajhőkülönbsége
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Állapotváltozás, I. főtétel |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Fejezzük ki a
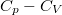 különbséget
különbséget  mol Van der Waals-gáz esetén a hőmérséklet, a térfogat és a
mol Van der Waals-gáz esetén a hőmérséklet, a térfogat és a 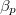 hőtágulási együttható segítségével!
hőtágulási együttható segítségével!
Megoldás
A termodinamika első főtételébe (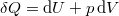 ) behelyettesítve az
) behelyettesítve az 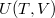 kétváltozós függvény teljes differenciálját
kétváltozós függvény teljes differenciálját
![\[ \delta Q = \left[ p + \left(\frac{\partial U}{\partial V}\right)_T \right] \,\mathrm{d}V + \left(\frac{\partial U}{\partial T}\right)_V \,\mathrm{d}T \]](/images/math/4/7/e/47e28e4d2ecb0595a776271f2fd8433b.png)
összefüggéshez, és ezt állandó nyomáson 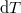 -vel formálisan osztva és a mólhők definícióját alkalmazva
-vel formálisan osztva és a mólhők definícióját alkalmazva
![\[ C_p- C_V = \frac{1}{n} \left[ p + \left(\frac{\partial U}{\partial V}\right)_T \right] \left(\frac{\partial V}{\partial T}\right)_p \]](/images/math/4/9/f/49fc1a0a58730f3ff5d1987ee330e6bf.png)
általános fajhőösszefüggéshez jutunk.
A Van der Waals-gáz belső energiáját leíró
![\[ U = n C_V T - n^2\frac{a}{V} \]](/images/math/5/6/6/56649fa9241afb399b4de7f1a348c9f3.png)
képletből kiszámíthatjuk
![\[ \left(\frac{\partial U}{\partial V}\right)_T = \frac{n^2a}{V^2} \]](/images/math/8/f/3/8f30c8ae997afcfbbc4f1521f522564c.png)
differenciálhányadost, és
![\[ \beta_p = \frac{1}{V} \left(\frac{\partial V}{\partial T}\right)_p \]](/images/math/c/5/b/c5bbb1f2f4680cbba379057eed004602.png)
definíciót beírhatjuk a fajhőösszefüggésbe:
![\[ C_p-C_V = \frac{1}{n} \left(p+\frac{n^2a}{V^2}\right) V \beta_p. \]](/images/math/0/a/3/0a382d8f209fd5bc7d12378a9b2dd02e.png)
A
![\[ \left(p+\frac{n^2a}{V^2}\right)\left(V-nb\right) = nRT \]](/images/math/e/9/d/e9d1173dc59a868ba08a25db27949ea0.png)
Van der Waals-gáz állapotegyenletből az első tényezőt kifejezve egyszerűbb kifejezéshez kapunk:
![\[ C_p-C_V = \frac{RT \beta_p}{\displaystyle 1-\frac{nb}{V}}. \]](/images/math/d/0/0/d000ed3518d8af2ee4ec1b59a3ffd611.png)