Termodinamika példák - Ideális gáz entrópiája

Feladat

1. Az ideális gáz entrópiáját gyakran az 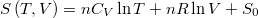$\setbox0\hbox{$S\left(T,V\right)=n C_V\ln T+nR\ln V+ S_0$}% \message{//depth:\the\dp0//}% \box0%$ alakban használják.
   • a) Indokolja meg, hogy az 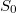$\setbox0\hbox{$S_0$}% \message{//depth:\the\dp0//}% \box0%$ mennyiségnek függnie kell a rendszer anyagmennyiségét megadó $\setbox0\hbox{$n$}% \message{//depth:\the\dp0//}% \box0%$ mólszámtól!
   • b) Adjon meg egy olyan 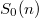$\setbox0\hbox{$S_0(n)$}% \message{//depth:\the\dp0//}% \box0%$-függést, amellyel az entrópia fenti kifejezése teljesíti az a) pontban szereplő követelményt!

Megoldás

a) Az entrópia extenzív mennyiség, ezért egy nagyobb rendszer entrópiája az őt alkotó (őt hiánytalanul tartalmazó, de diszjunkt) részrendszerek entrópiájának összege. Ez az additivitás csak úgy teljesülhet, ha az 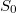$\setbox0\hbox{$S_0$}% \message{//depth:\the\dp0//}% \box0%$ referenciaérték függ a rendszer nagyságától, azaz a mólszámtól.

Megjegyzés

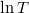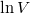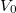A feladatban megadott képletben $\setbox0\hbox{$\ln T$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$\ln V$}% \message{//depth:\the\dp0//}% \box0%$ csak dimenzió nélkül (előre rögzített $\setbox0\hbox{$T_0$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$V_0$}% \message{//depth:\the\dp0//}% \box0%$ egységekben mért mértékegység nélküli számként) értelmezhetőek, ahogy az előző feladatban megállapítottuk:

$\[ S\left(T,V,n\right) - S_0(n) = n \left( C_V \ln T + R\ln V \right). \]$

b) Mivel az entrópia extenzív mennyiség, egyensúlyban felírható olyan tagokból, melyek pontosan egy extenzív mennyiséget (pl. mólszám) és intenzív mennyiségek függvényeit tartalmazzák. Intenzívnek tekintendőek a moláris- és sűrűségjellegű mennyiségek is.

Tegyük a térfogatot is molárissá, így leválaszthatjuk a mólszámtól való függést:

$\[ S\left(T,V,n\right) = n\left( C_V \ln T + R\ln \frac{V}{n} + R\ln n +\frac{S_0(n)}{n} \right) = n\left( C_V \ln T + R\ln V_M + s_0 \right), \]$

ahol a zárójelben intenzív mennyiségek állnak: 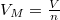$\setbox0\hbox{$ V_M = \frac{V}{n} $}% \message{//depth:\the\dp0//}% \box0%$ moláris térfogat és 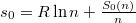$\setbox0\hbox{$ s_0 = R\ln n + \frac{S_0(n)}{n} $}% \message{//depth:\the\dp0//}% \box0%$ már függetlenek a mólszámtól, és beazonosíthatjuk, hogy

$\[ S_0(n)=-nR\ln n+ns_0. \]$