„Termodinamika példák - Kémiai potenciál hőmérsékletfüggése” változatai közötti eltérés
A Fizipedia wikiből
a (Szöveg koherenssé tétele) |
a (Szöveg koherensebbé tétele.) |
||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Ábrázoljuk (kvalitatív módon) egy tiszta anyag kémiai potenciáljának $\mu_p(T)$ hőmérsékletfüggését állandó nyomáson, az anyag szilárd-, folyadék- és gőzállapotát átfogó hőmérséklet-intervallumban! Az olvadáspontot $T_{olv}$-val, a forráspontot $T_{forr}$-ral jelöljük, és tegyük fel, hogy a mólentrópia egy fázison belül nem függ a hőmérséklettől!</wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk fel a $$\left(\frac{\partial G}{\partial T}\right)_p=-S$$ egyenletet, a kémiai potenciál és a szabad entalpia összefüggését, továbbá két fázis egyensúlyának feltételét.}}</wlatex></includeonly><noinclude> | + | </noinclude><wlatex># Ábrázoljuk (kvalitatív módon) egy tiszta anyag kémiai potenciáljának $\mu_p(T)$ hőmérsékletfüggését állandó nyomáson, az anyag szilárd-, folyadék- és gőzállapotát átfogó hőmérséklet-intervallumban! Az olvadáspontot $T_\text{olv}$-val, a forráspontot $T_\text{forr}$-ral jelöljük, és tegyük fel, hogy a mólentrópia egy fázison belül nem függ a hőmérséklettől!</wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk fel a $$\left(\frac{\partial G}{\partial T}\right)_p=-S$$ egyenletet, a kémiai potenciál és a szabad entalpia összefüggését, továbbá két fázis egyensúlyának feltételét.}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| 16. sor: | 16. sor: | ||
$$ \left(\frac{\partial G}{\partial T}\right)_p = -S $$ | $$ \left(\frac{\partial G}{\partial T}\right)_p = -S $$ | ||
összefüggést, amit most a moláris entrópia és kémiai potenciál kifejezésére használunk: | összefüggést, amit most a moláris entrópia és kémiai potenciál kifejezésére használunk: | ||
| − | $$ \left(\frac{\partial \mu }{\partial T}\right)_p = -\frac{S}{n} = -S_M $$ | + | $$ \left(\frac{\partial \mu }{\partial T}\right)_p = -\frac{S}{n} = -S_M. $$ |
| − | A | + | A szilárdból a folyadékon át a gőz halmazállapot felé haladva a halmazállapotok rendezetlenségének avagy a lehetséges a mikroállapotok „számának” növekedése miatt a mólentrópiáira fennáll, hogy: |
$$ S_M^\text{sz} < S_M^\text{foly.} < S_M^\text{gáz}, $$ | $$ S_M^\text{sz} < S_M^\text{foly.} < S_M^\text{gáz}, $$ | ||
amit most a halmazállapoton belül a mólentrópia hőmérsékletfüggetlenségével egészítünk ki: | amit most a halmazállapoton belül a mólentrópia hőmérsékletfüggetlenségével egészítünk ki: | ||
A lap jelenlegi, 2013. május 28., 20:46-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fázisátalakulások |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Ábrázoljuk (kvalitatív módon) egy tiszta anyag kémiai potenciáljának
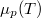hőmérsékletfüggését állandó nyomáson, az anyag szilárd-, folyadék- és gőzállapotát átfogó hőmérséklet-intervallumban! Az olvadáspontot 
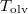-val, a forráspontot 
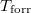-ral jelöljük, és tegyük fel, hogy a mólentrópia egy fázison belül nem függ a hőmérséklettől!
Megoldás
A differenciális összefüggésekről szóló feladatban tárgyaltuk a
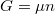szabadentalpiára vonatkozó
![\[ \left(\frac{\partial G}{\partial T}\right)_p = -S \]](/images/math/f/7/6/f76117a7dc87acddec129bb10fdbea45.png)
összefüggést, amit most a moláris entrópia és kémiai potenciál kifejezésére használunk:
![\[ \left(\frac{\partial \mu }{\partial T}\right)_p = -\frac{S}{n} = -S_M. \]](/images/math/a/e/9/ae93f9c9f01f436039378fb81ae9801b.png)
A szilárdból a folyadékon át a gőz halmazállapot felé haladva a halmazállapotok rendezetlenségének avagy a lehetséges a mikroállapotok „számának” növekedése miatt a mólentrópiáira fennáll, hogy:
![\[ S_M^\text{sz} < S_M^\text{foly.} < S_M^\text{gáz}, \]](/images/math/1/3/b/13b6c4eb03c4d1dcc425bafc3b0fa706.png)
amit most a halmazállapoton belül a mólentrópia hőmérsékletfüggetlenségével egészítünk ki:
![\[ \frac{\partial S_M}{\partial T} = 0. \]](/images/math/7/b/a/7baa1cac42149cf7a6f6f787285861cb.png)
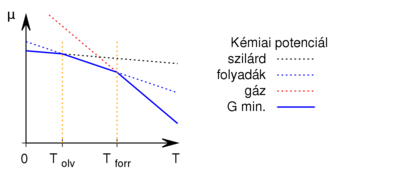
Ez alapján a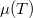 
grafikon egy töröttvonal, az anyag mindig a legalacsonyabb szabadentalpiájú fázist valósítja meg:
