„Termodinamika példák - Víz forráshőjének becslése” változatai közötti eltérés

A Fizipedia wikiből
 
(Lektori javaslatra a becslés pontosságát jelzem.)
 
(egy szerkesztő 3 közbeeső változata nincs mutatva)
10. sor: 10. sor:
 
== Feladat ==
 
== Feladat ==
 
</noinclude><wlatex># Ha a nyomást $\Delta p=0{,}1\,\mathrm{bar}$-ral megnöveljük, akkor a víz forrási hőmérséklete $\Delta T\approx 2{,}8\,\mathrm{\,^\circ C}$-kal növekszik. Ennek felhasználásával becsüljük meg a víz forráshőjét!</wlatex><includeonly><wlatex>{{Útmutatás|content=A vízgőzre alkalmazzuk az ideális gáz egyenletét, és hanyagoljuk el a víz fajlagos térfogatát a gőzéhez képest!}}{{Végeredmény|content=$$L_f\approx \frac{\Delta p}{\Delta T}\frac{RT^2}{p_kM}=2253\,\mathrm{\frac{kJ}{kg}}$$}}</wlatex></includeonly><noinclude>
 
</noinclude><wlatex># Ha a nyomást $\Delta p=0{,}1\,\mathrm{bar}$-ral megnöveljük, akkor a víz forrási hőmérséklete $\Delta T\approx 2{,}8\,\mathrm{\,^\circ C}$-kal növekszik. Ennek felhasználásával becsüljük meg a víz forráshőjét!</wlatex><includeonly><wlatex>{{Útmutatás|content=A vízgőzre alkalmazzuk az ideális gáz egyenletét, és hanyagoljuk el a víz fajlagos térfogatát a gőzéhez képest!}}{{Végeredmény|content=$$L_f\approx \frac{\Delta p}{\Delta T}\frac{RT^2}{p_kM}=2253\,\mathrm{\frac{kJ}{kg}}$$}}</wlatex></includeonly><noinclude>
 +
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>Megoldás szövege
+
<wlatex>A ''Clapeyron''-egyenlet linearizált alakja (ld. [[Termodinamika példák - Szilárd-folyadék átalakulás közelítő egyensúlyi görbéje|Szilárd-folyadék egyensúlyi görbe]])
 +
$$ \Delta p\approx \frac{L_M^\text{forr}}{\Delta V_M^\text{forr}}\frac{\Delta T}{T_1}, $$
 +
aminek segítségével kifejezzük a forráshőt. Felhasználva, hogy a gőz térfogatához képest a folyadék térfogatát elhanyagolhatjuk ($V_M^\text{gőz}\gg V_M^\text{foly}$), és a gőzt mint ideális gázt tekintve:
 +
$$ L_M^\text{forr} \approx  T_1\left(V_M^\text{gőz}- V_M^\text{foly}\right)\frac{\Delta p}{\Delta T}
 +
    \approx T_1 V_M^\text{gőz}\frac{\Delta p}{\Delta T}
 +
    = \frac{R T_1^2}{p_1}\frac{\Delta p}{\Delta T}. $$
 +
 
 +
Behelyettesítve a következő adatokat:
 +
$ \Delta p = 0{,}1\,\mathrm{bar} = 10\,\mathrm{kPa}$,
 +
$ \Delta T \approx 2{,}8\,\mathrm{\,^\circ C}$,
 +
$ T_1 = 373{,}15\,\mathrm{K}$,
 +
$ p_1 = 101\,325\,\mathrm{Pa}$,
 +
$ M = 18{,}01528\,\mathrm{\frac{g}{mol}}$,
 +
a forráshő becsült értéke:
 +
$$ L^\mathrm{forr} = \frac{L_M^\mathrm{forr}}{M}
 +
    \approx 2\,263\pm42\,\mathrm{\frac{kJ}{kg}}, $$ <!-- 2263,87 -->
 +
ami a közvetlen mérésből adódó $L^\text{forr} = 2\,256{,}37\,\mathrm{\frac{kJ}{kg}}$ érték jó közelítése. (A hibahatárt $T \approx 2{,}8\pm0{,}05\,\mathrm{\,^\circ C}$ mérési pontosságot feltételezve becsültük.)
 +
 
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap jelenlegi, 2013. szeptember 20., 14:18-kori változata

[rejt] Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Fázisátalakulások
Feladatok listája:
  1. Izobár átalakulási hő
  2. Elforralás
  3. Telített gőz dugattyúban
  4. Kémiai potenciál
  5. Olvadáspont eltolódása
  6. Szil-foly átalak. görbéje
  7. Olvadáshő becslése
  8. Víz forráshője
  9. Argon olvadási görbéje
  10. Fázisok egyensúlya
  11. Fázisátalakulások rendje
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

  1. Ha a nyomást 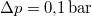\setbox0\hbox{$\Delta p=0{,}1\,\mathrm{bar}$}% \message{//depth:\the\dp0//}% \box0%-ral megnöveljük, akkor a víz forrási hőmérséklete 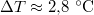\setbox0\hbox{$\Delta T\approx 2{,}8\,\mathrm{\,^\circ C}$}% \message{//depth:\the\dp0//}% \box0%-kal növekszik. Ennek felhasználásával becsüljük meg a víz forráshőjét!

Megoldás

A Clapeyron-egyenlet linearizált alakja (ld. Szilárd-folyadék egyensúlyi görbe)

\[ \Delta p\approx \frac{L_M^\text{forr}}{\Delta V_M^\text{forr}}\frac{\Delta T}{T_1}, \]

aminek segítségével kifejezzük a forráshőt. Felhasználva, hogy a gőz térfogatához képest a folyadék térfogatát elhanyagolhatjuk (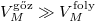\setbox0\hbox{$V_M^\text{gőz}\gg V_M^\text{foly}$}% \message{//depth:\the\dp0//}% \box0%), és a gőzt mint ideális gázt tekintve:

\[ L_M^\text{forr} \approx T_1\left(V_M^\text{gőz}- V_M^\text{foly}\right)\frac{\Delta p}{\Delta T} \approx T_1 V_M^\text{gőz}\frac{\Delta p}{\Delta T} = \frac{R T_1^2}{p_1}\frac{\Delta p}{\Delta T}. \]

Behelyettesítve a következő adatokat: 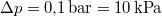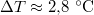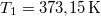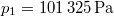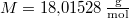\setbox0\hbox{$ \Delta p = 0{,}1\,\mathrm{bar} = 10\,\mathrm{kPa}$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$ \Delta T \approx 2{,}8\,\mathrm{\,^\circ C}$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$ T_1 = 373{,}15\,\mathrm{K}$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$ p_1 = 101\,325\,\mathrm{Pa}$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$ M = 18{,}01528\,\mathrm{\frac{g}{mol}}$}% \message{//depth:\the\dp0//}% \box0%, a forráshő becsült értéke:

\[ L^\mathrm{forr} = \frac{L_M^\mathrm{forr}}{M} \approx 2\,263\pm42\,\mathrm{\frac{kJ}{kg}}, \]

ami a közvetlen mérésből adódó 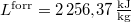\setbox0\hbox{$L^\text{forr} = 2\,256{,}37\,\mathrm{\frac{kJ}{kg}}$}% \message{//depth:\the\dp0//}% \box0% érték jó közelítése. (A hibahatárt 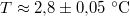\setbox0\hbox{$T \approx 2{,}8\pm0{,}05\,\mathrm{\,^\circ C}$}% \message{//depth:\the\dp0//}% \box0% mérési pontosságot feltételezve becsültük.)


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Termodinamika_példák_-_Víz_forráshőjének_becslése&oldid=12757”