„Termodinamika példák - Argon olvadási görbéje” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Termodinamika - Fázisátalakulások {{Kísérleti fizika g…”) |
a (Lektori javaslatra utalok törvényszerűségek közelítő jellegére) |
||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># A szilárd argon $p_0=1\,\mathrm{bar}$ | + | </noinclude><wlatex># A szilárd argon $p_0=1\,\mathrm{bar}$ nyomáson $ T_0=83\,\mathrm{K}$ hőmérsékleten olvad meg. Olvadáshője ekkor $L_M^\text{olv}=1176\,\mathrm{\frac{J}{mol}}$, móltérfogatának változása $\Delta V_{M0}=3{,}5\,\mathrm{\frac{cm^3}{mol}}$. A nyomás növekedésekor kísérleti eredmények szerint az olvadáshő nem változik, a $\Delta V_M$ móltérfogatváltozás viszont az abszolút hőmérséklet megközelítőleg $3/2$-ik hatványával arányos.<br />Mekkora nyomást kell alkalmaznunk ahhoz, hogy az olvadási hőmérséklet megkétszereződjék? |
| − | </wlatex><includeonly><wlatex>{{Útmutatás|content=A $\Delta v$ hőmérsékletfüggésének figyelembevételével integráljuk a Clausius-Clapeyron-egyenletet!}}{{Végeredmény|content=$$p | + | </wlatex><includeonly><wlatex>{{Útmutatás|content=A $\Delta v$ hőmérsékletfüggésének figyelembevételével integráljuk a Clausius-Clapeyron-egyenletet!}}{{Végeredmény|content=$$p=p_0+\frac{2L}{3\Delta v_0}\left(1-\left(\frac{T_0}{T}\right)^{3/2}\right)=1449\,\mathrm{bar}$$}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>A móltérfogat |
| + | $$ \Delta V_M = \Delta V_{M0} \left(\frac{T}{T_0}\right)^{3/2} $$ | ||
| + | hőmérsékletfüggését behelyettesítjük a Clapeyron-egyenletbe | ||
| + | $$ \frac{\mathrm{d}p}{\mathrm{d}T} = \frac{L_M^\text{olv} T_0^{3/2}}{T^{5/2} \Delta V_{M0}^\text{olv}}. $$ | ||
| + | Ezt változószétválasztás után integrálva $p_0$ és $p$ illetve $T_0$ és $T_1=2T_0$ között: | ||
| + | $$ p = p_0+\frac{L_M^\text{olv} T_0^{3/2}}{\Delta V_{M0}} \left[-\frac23 T^{-3/2}\right]_{T_0}^{2 T_0} | ||
| + | = p_0+\frac23\frac{L_M^\text{olv}}{\Delta V_{M0}}\left(1-\left(\frac12\right)^{3/2}\right) | ||
| + | \approx 1449\,\mathrm{bar}. $$ | ||
| + | |||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. szeptember 20., 13:34-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fázisátalakulások |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- A szilárd argon
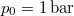nyomáson 
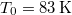hőmérsékleten olvad meg. Olvadáshője ekkor 
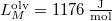, móltérfogatának változása 
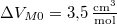. A nyomás növekedésekor kísérleti eredmények szerint az olvadáshő nem változik, a 
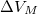móltérfogatváltozás viszont az abszolút hőmérséklet megközelítőleg 
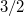-ik hatványával arányos.
Mekkora nyomást kell alkalmaznunk ahhoz, hogy az olvadási hőmérséklet megkétszereződjék?
Megoldás
A móltérfogat
![\[ \Delta V_M = \Delta V_{M0} \left(\frac{T}{T_0}\right)^{3/2} \]](/images/math/b/d/1/bd1c176a5dfd875ab8a60f062f52266b.png)
hőmérsékletfüggését behelyettesítjük a Clapeyron-egyenletbe
![\[ \frac{\mathrm{d}p}{\mathrm{d}T} = \frac{L_M^\text{olv} T_0^{3/2}}{T^{5/2} \Delta V_{M0}^\text{olv}}. \]](/images/math/a/a/b/aabccc74c95b7068dea9e02c1098e65a.png)
Ezt változószétválasztás után integrálva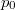 
és 
illetve 
és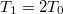 
között:
![\[ p = p_0+\frac{L_M^\text{olv} T_0^{3/2}}{\Delta V_{M0}} \left[-\frac23 T^{-3/2}\right]_{T_0}^{2 T_0} = p_0+\frac23\frac{L_M^\text{olv}}{\Delta V_{M0}}\left(1-\left(\frac12\right)^{3/2}\right) \approx 1449\,\mathrm{bar}. \]](/images/math/b/b/5/bb5c77b82e5c946024ab298a77c6b42b.png)
