„Termodinamika - Állapotváltozás, I. főtétel” változatai közötti eltérés
A Fizipedia wikiből
a (→Ismert összefüggések: Lektori javaslatra bővítem az összefoglalót.) |
|||
| (egy szerkesztő 12 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | < | + | <noinclude> |
| − | + | ||
[[Kategória:Kísérleti fizika 3. gyakorlat]] | [[Kategória:Kísérleti fizika 3. gyakorlat]] | ||
[[Kategória:Szerkesztő:Stippinger]] | [[Kategória:Szerkesztő:Stippinger]] | ||
| − | |||
| − | |||
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika 3. gyakorlat | | tárgynév = Kísérleti fizika 3. gyakorlat | ||
| gyaksorszám = 2 | | gyaksorszám = 2 | ||
| − | | témakör = Termodinamika - Állapotváltozás, I. főtétel|Állapotváltozás, I. főtétel | + | | témakör = Termodinamika - Állapotváltozás, I. főtétel |
| − | | | + | | rövid = Állapotváltozás, I. főtétel |
| − | + | | fejezetlap = true | |
}} | }} | ||
| + | == Ismert összefüggések == | ||
| + | <wlatex>'''A termodinamika I. főtétele''' | ||
| + | $$ \mathrm{d}U = \delta Q + \delta W, $$ | ||
| + | ahol $\mathrm{d}U$ a rendszer belső energiájának megváltozása, $\delta Q$ a rendszer által felvett hő, $\delta W$ a rendszeren a környezet által végzett makroszkopikus munka, például $\delta W_\text{mech} = -p\,\mathrm{d}V$. | ||
| + | |||
| + | '''A ''Van der Waals''-gáz állapotegyenlete''' | ||
| + | $$ \left(p+n^2\frac{a}{V^2}\right)(V-nb) = nRT, $$ | ||
| + | ahol $p_k = n^2\frac{a}{V^2}$ kohéziós nyomás, $V-nb$ tiszta térfogat, $a$ és $b$ kísérletileg meghatározható állandók. | ||
| + | |||
| + | '''Mérhető mennyiségek''' | ||
| + | |||
| + | A tanult $C_V$, $C_p$, $\beta$, $\kappa_T$ és $\kappa_S$ definíciókat a [[Termodinamika - Homogén rendszerek|Homogén rendszerek]] fejezet elején foglaljuk össze. | ||
| + | $\gamma$-val jelöljük a $C_p/C_V$ fajhőviszonyt. | ||
| + | </wlatex> | ||
| − | + | == Feladatok == | |
| − | + | </noinclude> | |
| − | + | {{:Termodinamika példák - Állapotváltozások diagramjai}}{{Megoldás|link=Termodinamika példák - Állapotváltozások diagramjai}} | |
| − | + | {{:Termodinamika példák - Belső energia az állapotváltozások során}}{{Megoldás|link=Termodinamika példák - Belső energia az állapotváltozások során}} | |
| − | + | {{:Termodinamika példák - Energia-összefüggések fajhőviszonnyal}}{{Megoldás|link=Termodinamika példák - Energia-összefüggések fajhőviszonnyal}} | |
| − | + | {{:Termodinamika példák - Energiaváltozások diagramból}}{{Megoldás|link=Termodinamika példák - Energiaváltozások diagramból}} | |
| − | + | {{:Termodinamika példák - Ideális gáz kompresszibilitásai}}{{Megoldás|link=Termodinamika példák - Ideális gáz kompresszibilitásai}} | |
| + | {{:Termodinamika példák - Nyomás hőmérsékletfüggése mérhető mennyiségekkel}}{{Megoldás|link=Termodinamika példák - Nyomás hőmérsékletfüggése mérhető mennyiségekkel}} | ||
| + | {{:Termodinamika példák - Fűtött szoba belső energiája}}{{Megoldás|link=Termodinamika példák - Fűtött szoba belső energiája}} | ||
| + | {{:Termodinamika példák - Térfogatváltozás fajhőviszonnyal}}{{Megoldás|link=Termodinamika példák - Térfogatváltozás fajhőviszonnyal}} | ||
| + | {{:Termodinamika példák - Van der Waals-gáz egyensúlyi hőmérséklete}}{{Megoldás|link=Termodinamika példák - Van der Waals-gáz egyensúlyi hőmérséklete}} | ||
| + | {{:Termodinamika példák - Kondenzált anyag közelítő állapotegyenlete}}{{Megoldás|link=Termodinamika példák - Kondenzált anyag közelítő állapotegyenlete}} | ||
| + | {{:Termodinamika példák - Szilárd testek közelítő állapotegyenlete mérhető mennyiségekből}}{{Megoldás|link=Termodinamika példák - Szilárd testek közelítő állapotegyenlete mérhető mennyiségekből}} | ||
| + | {{:Termodinamika példák - Van der Waals-gáz fajhőkülönbsége}}{{Megoldás|link=Termodinamika példák - Van der Waals-gáz fajhőkülönbsége}} | ||
A lap jelenlegi, 2013. szeptember 20., 14:39-kori változata
Ismert összefüggések
A termodinamika I. főtétele
![\[ \mathrm{d}U = \delta Q + \delta W, \]](/images/math/5/4/9/5493a20ea4cdfb814f1ebff515cbfccd.png)
ahol 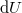 a rendszer belső energiájának megváltozása,
a rendszer belső energiájának megváltozása, 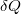 a rendszer által felvett hő,
a rendszer által felvett hő, 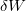 a rendszeren a környezet által végzett makroszkopikus munka, például
a rendszeren a környezet által végzett makroszkopikus munka, például 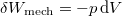 .
.
A Van der Waals-gáz állapotegyenlete
![\[ \left(p+n^2\frac{a}{V^2}\right)(V-nb) = nRT, \]](/images/math/9/3/7/937e67f72fe5b57c46c75e12722b530a.png)
ahol 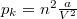 kohéziós nyomás,
kohéziós nyomás, 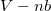 tiszta térfogat,
tiszta térfogat,  és
és  kísérletileg meghatározható állandók.
kísérletileg meghatározható állandók.
Mérhető mennyiségek
A tanult 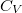 ,
, 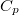 ,
,  ,
, 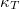 és
és 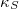 definíciókat a Homogén rendszerek fejezet elején foglaljuk össze.
definíciókat a Homogén rendszerek fejezet elején foglaljuk össze.
 -val jelöljük a
-val jelöljük a 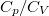 fajhőviszonyt.
fajhőviszonyt.
Feladatok
- Készítsen vázlatos ábrát ideális gáz
- a) izochor,
- b) izobár,
- c) izoterm és
- d) adiabatikus
- állapotváltozásáról
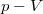 ,
, 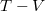 és
és 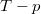 koordináta-rendszerekben úgy, hogy a kiindulási állapot minden esetben ugyanaz legyen!
koordináta-rendszerekben úgy, hogy a kiindulási állapot minden esetben ugyanaz legyen!
- Ábrázolja vázlatosan ideális gáz
- a) izochor,
- b) izobár,
- c) izoterm és
- d) adiabatikus
- állapotváltozásánál a belső energiának a hőmérséklettől-, térfogattól- és a nyomástól való függését! Legyen a belső energia az ordináta, és minden folyamatnál legyen ugyanaz a kiindulási állapot!
- Állapítsuk meg, milyen összefüggés van egy ideális gáz által állandó nyomáson végzett
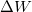 munka, a gázzal közölt
munka, a gázzal közölt 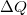 hőmennyiség és a
hőmennyiség és a 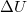 belső energia-változás között, ha a
belső energia-változás között, ha a  fajhőviszony ismert!
fajhőviszony ismert!
- Ha egy rendszert az ábrán látható 1 úton viszünk az
 állapotból a
állapotból a  állapotba,
állapotba, 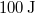 hőt vesz fel, miközben
hőt vesz fel, miközben 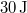 munkát végez.
munkát végez.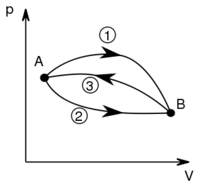
- a) Mennyi hőt vesz fel a rendszer az
 és
és  állapotok közt a 2 úton, ha közben
állapotok közt a 2 úton, ha közben 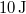 munkát végez?
munkát végez?
- b) Ha
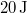 munkával vihetjük a rendszert
munkával vihetjük a rendszert  -ből
-ből  -ba a 3 út mentén, mennyi a közben leadott hő?
-ba a 3 út mentén, mennyi a közben leadott hő?
- a) Mennyi hőt vesz fel a rendszer az
- Mutassa meg, hogy ideális gáz izoterm összenyomásánál a kompresszibilitás
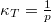 , míg adiabatikus összenyomásnál
, míg adiabatikus összenyomásnál 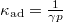 , ahol
, ahol 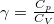 .
.
- A
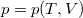 állapotegyenlet ismeretében fejezzük ki a
állapotegyenlet ismeretében fejezzük ki a 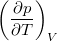 mennyiséget a
mennyiséget a 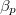 hőtágulási együttható és a
hőtágulási együttható és a 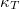 izotermikus kompresszibilitás segítségével!
izotermikus kompresszibilitás segítségével!
- Egy
 térfogatú szobában befűtünk. A szobában a hőmérséklet eközben állandó légköri nyomáson
térfogatú szobában befűtünk. A szobában a hőmérséklet eközben állandó légköri nyomáson  -ről
-ről 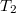 -re nő. Mennyivel változik a szobában lévő levegő belső energiája?
-re nő. Mennyivel változik a szobában lévő levegő belső energiája?
- Egy kezdetben
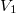 térfogatú,
térfogatú,  fajhőviszonyú ideális gáz térfogatát
fajhőviszonyú ideális gáz térfogatát 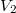 -re növeljük. A folyamatot egyszer adiabatikusan, másodszor pedig izotermikusan hajtjuk végre. Az első és második végállapotban a nyomások aránya
-re növeljük. A folyamatot egyszer adiabatikusan, másodszor pedig izotermikusan hajtjuk végre. Az első és második végállapotban a nyomások aránya  . Mekkora a
. Mekkora a 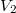 térfogat?
térfogat?
- Van der Waals-gázok belső energiájának térfogatfüggése az alábbi összefüggéssel adható meg: ahol
![\[ U = c_V mT - \frac{m^2}{M^2}\frac{a}{V},\]](/images/math/b/4/7/b47f383e5a17bd995a4937b18f1989c8.png)
 a gáz tömege,
a gáz tömege,  a móltömeg,
a móltömeg, 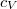 az állandó térfogaton mért fajhő,
az állandó térfogaton mért fajhő,  állandó.
állandó.
Egy hőszigetelt tartályt rögzített, jó hővezető anyagból készített fal választ két részre, amelyekbe azonos tömegű Van der Waals-gázt vezettünk be. A kezdeti állapotjellemzők: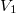 ,
,  , illetve
, illetve 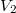 ,
, 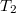 .
.
- a) Mennyi lesz a végső egyensúlyi hőmérséklet?
- b) Hogyan módosul a válasz, ha a gáz betöltése után az elválasztó falat rögtön kivesszük?
- Kondenzált (folyadék vagy szilárd) anyagok egyik közelítő állapotegyenlete Mi az
![\[V= V_0(1-ap+bT).\]](/images/math/3/2/d/32dfd83af77dc0541a76a1b499f794f8.png)
 és
és  paraméterek jelentése?
paraméterek jelentése?
- Szilárd testek hőtágulási együtthatója, illetve izotermikus kompresszibilitása alacsony hőmérsékleten az alábbi összefüggésekkel adható meg: (
![\[ \beta_p = \frac{3aT^3}{V},\qquad \kappa_T=\frac{b}{V} \]](/images/math/c/4/5/c452cee6e528e707dc57f0f8a8cb00da.png)
 és
és  állandók). Határozzuk meg a szilárd test ilyenkor érvényes állapotegyenletét!
állandók). Határozzuk meg a szilárd test ilyenkor érvényes állapotegyenletét!
- Fejezzük ki a
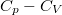 különbséget
különbséget  mol Van der Waals-gáz esetén a hőmérséklet, a térfogat és a
mol Van der Waals-gáz esetén a hőmérséklet, a térfogat és a 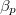 hőtágulási együttható segítségével!
hőtágulási együttható segítségével!
![\[\Delta Q = \frac{\gamma}{\gamma-1}\Delta W = \gamma \Delta U\]](/images/math/8/5/b/85be9e56262f39a875414a126cad154e.png)
![\[\Delta Q = 80\,\rm{J}\]](/images/math/5/c/e/5ce69d1df43da9c44332675f00e619cb.png)
![\[\Delta Q = 90\,\rm{J}\]](/images/math/0/8/c/08ce50a287cbb333107df509b4469cb7.png)
![\[\kappa_{\mathit{ad}}=\frac{1}{\gamma p}\]](/images/math/1/f/e/1feb5ea49c75fe40f04869aa24729ef9.png)
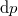 teljes differenciál nulla.
teljes differenciál nulla. ![\[{\left(\frac{\partial p}{\partial T}\right)}_V = \frac{\beta_p}{\kappa_T}\]](/images/math/e/4/9/e496792ff87f32233de1607c8704883d.png)
![\[V_2=V_1\,2\frac{1}{\gamma-1}\]](/images/math/7/d/5/7d587d64171a43d070331fc0db59c195.png)
![\[T=\frac{T_1+T_2}{2}\]](/images/math/4/5/d/45d22e35974fa6f3871ee196153942fb.png)
![\[T=\frac{T_1+T_2}{2}-\frac{ma\left(V_1-V_2\right)^2}{2M^2c_VV_1V_2\left(V_1+V_2\right)}\]](/images/math/7/9/5/795c653443761983b2ab64515717f29d.png)
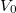 térfogatnál érvényes izotermikus kompresszibilitás és hőtágulási együttható.
térfogatnál érvényes izotermikus kompresszibilitás és hőtágulási együttható. ![\[p=\frac{3a}{4b}T^4+\frac{V_0-V}{b},\]](/images/math/f/0/3/f03818c4d7f756ea3d47cd7ddb4bed96.png)
![\[C_p-C_V=\frac{1}{n}\left(p+\left(\frac{\partial U}{\partial V}\right)_T\right)\left(\frac{\partial V}{\partial T}\right)_p\]](/images/math/c/3/4/c342b7595e6daf4375e0a9e1fafdf029.png)
![\[C_p-C_V=\frac{RT\beta_p}{1-nb/V}.\]](/images/math/a/7/4/a746f69df3bc690df6825fc3ea6c9d2d.png)