„Magnetosztatika példák - Egyenes vezető mágneses tere” változatai közötti eltérés
| (egy szerkesztő 14 közbeeső változata nincs mutatva) | |||
| 2. sor: | 2. sor: | ||
[[Kategória:Kísérleti fizika gyakorlat 2.]] | [[Kategória:Kísérleti fizika gyakorlat 2.]] | ||
[[Kategória:Szerkesztő:Beleznai]] | [[Kategória:Szerkesztő:Beleznai]] | ||
| − | [[Kategória: | + | [[Kategória:Magnetosztatika2]] |
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika gyakorlat 2. | | tárgynév = Kísérleti fizika gyakorlat 2. | ||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex>#Határozzuk meg egy $I$ áram által átjárt véges hosszúságú egyenes vezető mágneses terét a vezetőtől $d$ távolságra található az $O$ pontban. A vezető szakasz egyik vége $O$ pontból $\alpha_1$, míg a másik vége $\alpha_2$ szög alatt látszódik az $O$-ból a vezetőre állított merőlegeshez képest.</wlatex><includeonly><wlatex>{{Végeredmény|content=$$ | + | </noinclude><wlatex>#Határozzuk meg egy $I$ áram által átjárt véges hosszúságú egyenes vezető mágneses terét a vezetőtől $d$ távolságra található az $O$ pontban. A vezető szakasz egyik vége $O$ pontból $\alpha_1$, míg a másik vége $\alpha_2$ szög alatt látszódik az $O$-ból a vezetőre állított merőlegeshez képest.</wlatex><includeonly><wlatex>{{Végeredmény|content=$$B=\dfrac{\mu_0 I}{4 \pi d} (1-(-1))=\dfrac{\mu_0 I}{2 \pi d}$$}}</wlatex></includeonly><noinclude> |
| − | </wlatex></includeonly><noinclude> | + | |
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
a.) A mágneses tér meghatározható, ha a Biot-Savart törvényt kiintegráljuk a vezető teljes hossza mentén: | a.) A mágneses tér meghatározható, ha a Biot-Savart törvényt kiintegráljuk a vezető teljes hossza mentén: | ||
| − | $$B=\ | + | $$B=\frac{\mu_0 I}{4 \pi} \int \frac{\vec{dl}\times \vec{r}}{\mid \vec{r} \mid ^3}$$ |
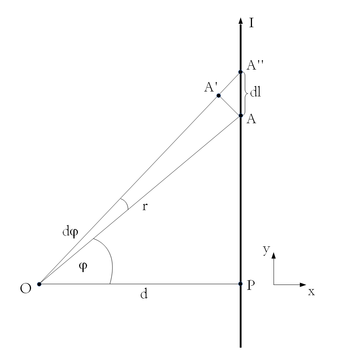
| − | Ahol $dl$ az áramjárta vezető elemi darabja, $r$ pedig az elemi vezetődarabtól a tér vizsgált pontjába mutató vektor. A tér vizsgált pontját nevezzük ki a koordináta-rendszer origójának ($O$). Ettől $d$ távolságra, az $y$ tengellyel párhuzamosan helyezkedik el az áramjárta vezető. Parametrizáljuk a vezető pontjait a vezető adott pontjából az origóba húzott $r$ sugár $x$ tengellyel bezárt $\varphi$ szögével az ábra szerint. | + | Ahol $dl$ az áramjárta vezető elemi darabja, $r$ pedig az elemi vezetődarabtól a tér vizsgált pontjába mutató vektor. A tér vizsgált pontját nevezzük ki a koordináta-rendszer origójának ($O$). Ettől $d$ távolságra, az $y$ tengellyel párhuzamosan helyezkedik el az áramjárta vezető. Parametrizáljuk a vezető pontjait a vezető adott pontjából az origóba húzott $r$ sugár $x$ tengellyel bezárt $\varphi$ szögével az ábra szerint.(ábra) |
| − | + | ||
| + | [[Kép:KFGY2-6-1uj.png|none|350px]] | ||
Fejezzünk ki a Biot-Savart integrál változóit $\varphi$ függvényében! | Fejezzünk ki a Biot-Savart integrál változóit $\varphi$ függvényében! | ||
| 31. sor: | 31. sor: | ||
$$dl=\dfrac{AA'}{\cos (\varphi)}=\dfrac{r}{\cos(\varphi)}d\varphi=\dfrac{d}{\cos^2(\varphi)}d\varphi$$ | $$dl=\dfrac{AA'}{\cos (\varphi)}=\dfrac{r}{\cos(\varphi)}d\varphi=\dfrac{d}{\cos^2(\varphi)}d\varphi$$ | ||
| − | A Biot-Savart törvényben szereplő vektorszorzat a vezető minden $dl$ eleme esetén az ábra síkjára merőleges, | + | A Biot-Savart törvényben szereplő vektorszorzat a vezető minden $dl$ eleme esetén az ábra síkjára merőleges, kifelé mutató mágneses indukció járulékot ad az $O$ pontban. Emiatt a vektorszorzatot az alábbiak szerint egyszerűsíthetjük: |
| − | $$B=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{\mid dl\ \mid \mid r \mid sin(A'' | + | $$B=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{\mid dl\ \mid \mid r \mid sin(A''AO)}{\mid r \mid ^3}=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{\mid dl\ \mid sin(A''AO)}{\mid r \mid ^2}=$$ |
| − | $$=\dfrac{\mu_0 I}{4 \pi} \int_{\alpha_1}^{\alpha_2} \dfrac{ \left( \dfrac{d}{\cos^2(\varphi)} \right) sin(A'' | + | $$=\dfrac{\mu_0 I}{4 \pi} \int_{\alpha_1}^{\alpha_2} \dfrac{ \left( \dfrac{d}{\cos^2(\varphi)} \right) sin(A''AO)}{ \left( \dfrac{d}{\cos(\varphi)} \right)^2 }d\varphi=\dfrac{\mu_0 I}{4 \pi} \int_{\alpha_1}^{\alpha_2} \dfrac{ sin(A''AO)}{ d }d\varphi$$ |
| − | Az ábra alapján a szinusz argumentumában szereplő $A'' | + | Az ábra alapján a szinusz argumentumában szereplő $A''AO$ szögről beláthatjuk, hogy: |
| − | $$A'' | + | $$A''AO=180-OAP=180-(90-\varphi)=90+\varphi$$ |
Tehát: | Tehát: | ||
| − | $$\sin(A'' | + | $$\sin(A''AO)=\cos(\varphi)$$ |
A Biot-Savart integrál tehát tovább egyszerűsödik: | A Biot-Savart integrál tehát tovább egyszerűsödik: | ||
| 57. sor: | 57. sor: | ||
Megjegyzés | Megjegyzés | ||
| − | Az eredményt érdemes megjegyezni, hiszen a későbbiekben gyakran találkozunk olyan áramjárta vezető | + | Az eredményt érdemes megjegyezni, hiszen a későbbiekben gyakran találkozunk olyan áramjárta vezető elrendezésekkel, melyek véges egyenes szakaszokból tevődnek össze. Külön figyelmet érdemel a végtelen vezetőre vonatkozó határeset, amikor $\alpha_1=\pi /2$ és $\alpha_2=-\pi /2$. Ilyenkor a tér: |
$$B=\dfrac{\mu_0 I}{4 \pi d} (1-(-1))=\dfrac{\mu_0 I}{2 \pi d}$$ | $$B=\dfrac{\mu_0 I}{4 \pi d} (1-(-1))=\dfrac{\mu_0 I}{2 \pi d}$$ | ||
| − | Az eredmény megnyugtató összhangban van a végtelen egyenes vezető Amper-féle gerjesztési törvénnyel kiszámolt terével: [[Magnetosztatika példák - Egyenes vezető mágneses tere 2|Egyenes vezető mágneses tere 2]] | + | Az eredmény megnyugtató összhangban van a végtelen egyenes vezető Amper-féle gerjesztési törvénnyel kiszámolt terével: [[Magnetosztatika példák - Egyenes vezető mágneses tere 2|Egyenes vezető mágneses tere 2]] |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. szeptember 30., 16:43-kori változata
Feladat
- Határozzuk meg egy
áram által átjárt véges hosszúságú egyenes vezető mágneses terét a vezetőtől 
távolságra található az 
pontban. A vezető szakasz egyik vége pontból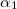 
, míg a másik vége 
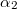szög alatt látszódik az -ból a vezetőre állított merőlegeshez képest.
Megoldás
a.) A mágneses tér meghatározható, ha a Biot-Savart törvényt kiintegráljuk a vezető teljes hossza mentén:
![\[B=\frac{\mu_0 I}{4 \pi} \int \frac{\vec{dl}\times \vec{r}}{\mid \vec{r} \mid ^3}\]](/images/math/3/e/9/3e9a20b8689b5013babc48b359a638d8.png)
Ahol 
az áramjárta vezető elemi darabja, 
pedig az elemi vezetődarabtól a tér vizsgált pontjába mutató vektor. A tér vizsgált pontját nevezzük ki a koordináta-rendszer origójának (). Ettől távolságra, az 
tengellyel párhuzamosan helyezkedik el az áramjárta vezető. Parametrizáljuk a vezető pontjait a vezető adott pontjából az origóba húzott sugár 
tengellyel bezárt 
szögével az ábra szerint.(ábra)
Fejezzünk ki a Biot-Savart integrál változóit függvényében!
![\[r=\dfrac{d}{\cos (\varphi)}\]](/images/math/6/1/b/61b954394b9f4891b355e903c60ee651.png)
Az 
és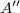 
pontok közti infinitezimális vezetőszakasz az pontból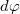 
szög alatt látszik. Az 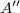szakaszon kijelölünk egy 
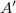pontot úgy, hogy 
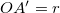. Belátható, hogy az 
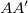szakasz hossza közelítőleg megegyezik egy 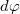szög alatt látszó sugarú ívelemmel:
![\[ AA'=r d\varphi\]](/images/math/f/a/a/faa921e8633f021cb09cded213b4b306.png)
Mivel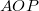 
és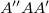 
merőleges szárú szögek, ezért 
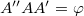. Ezek alapján:
![\[dl=\dfrac{AA'}{\cos (\varphi)}=\dfrac{r}{\cos(\varphi)}d\varphi=\dfrac{d}{\cos^2(\varphi)}d\varphi\]](/images/math/6/c/6/6c60c316e1ee6c57930bb58c33328e94.png)
A Biot-Savart törvényben szereplő vektorszorzat a vezető minden eleme esetén az ábra síkjára merőleges, kifelé mutató mágneses indukció járulékot ad az pontban. Emiatt a vektorszorzatot az alábbiak szerint egyszerűsíthetjük:
![\[B=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{\mid dl\ \mid \mid r \mid sin(A''AO)}{\mid r \mid ^3}=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{\mid dl\ \mid sin(A''AO)}{\mid r \mid ^2}=\]](/images/math/6/7/5/6752d15140d0ce5a5c2fc639df973999.png)
![\[=\dfrac{\mu_0 I}{4 \pi} \int_{\alpha_1}^{\alpha_2} \dfrac{ \left( \dfrac{d}{\cos^2(\varphi)} \right) sin(A''AO)}{ \left( \dfrac{d}{\cos(\varphi)} \right)^2 }d\varphi=\dfrac{\mu_0 I}{4 \pi} \int_{\alpha_1}^{\alpha_2} \dfrac{ sin(A''AO)}{ d }d\varphi\]](/images/math/4/f/9/4f9f4cdf7068abd0d0ecfff5ef544062.png)
Az ábra alapján a szinusz argumentumában szereplő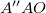 
szögről beláthatjuk, hogy:
![\[A''AO=180-OAP=180-(90-\varphi)=90+\varphi\]](/images/math/5/f/7/5f7180140294a1e7759d24e3da9f0a38.png)
Tehát:
![\[\sin(A''AO)=\cos(\varphi)\]](/images/math/6/0/1/601693d77851c31b5460666891a94c6c.png)
A Biot-Savart integrál tehát tovább egyszerűsödik:
![\[B=\dfrac{\mu_0 I}{4 \pi d} \int_{\alpha_1}^{\alpha_2} cos(\varphi) d\varphi =\dfrac{\mu_0 I}{4 \pi d}\left( \sin(\alpha_1)-sin(\alpha_2) \right) \]](/images/math/2/e/e/2ee825f2020fb089688e7bb7b4d507a8.png)
A véges hosszúságú áramjárta vezető mágneses terének nagysága tehát:
![\[B=\dfrac{\mu_0 I}{4 \pi d}\left( \sin(\alpha_1)-sin(\alpha_2) \right) \]](/images/math/d/5/e/d5e2c5942590a6749630b837801a8625.png)
Iránya pedig az ábra síkjára merőlegesen kifelé mutat.
Megjegyzés
Az eredményt érdemes megjegyezni, hiszen a későbbiekben gyakran találkozunk olyan áramjárta vezető elrendezésekkel, melyek véges egyenes szakaszokból tevődnek össze. Külön figyelmet érdemel a végtelen vezetőre vonatkozó határeset, amikor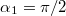 
és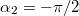 
. Ilyenkor a tér:
![\[B=\dfrac{\mu_0 I}{4 \pi d} (1-(-1))=\dfrac{\mu_0 I}{2 \pi d}\]](/images/math/8/5/3/853f065bc278c152dca55b624e44abc8.png)
Az eredmény megnyugtató összhangban van a végtelen egyenes vezető Amper-féle gerjesztési törvénnyel kiszámolt terével: Egyenes vezető mágneses tere 2
