„Termodinamika példák - Stern-kísérlet” változatai közötti eltérés
(Új oldal, tartalma: „Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Termodinamika - Kinetikus gázelmélet, transzportfolyamatok {{Kísér…”) |
|||
| 22. sor: | 22. sor: | ||
* b) Milyen sebességnél adják a legnagyobb rétegvastagságot a külső hengerfelületen lecsapódó ezüstatomok? Útmutatás: Az időegység alatt lecsapódó részecskék számát határozzuk meg a Maxwell-eloszlás alapján, és használjuk ki az $x\sim 1/v$ összefüggést. | * b) Milyen sebességnél adják a legnagyobb rétegvastagságot a külső hengerfelületen lecsapódó ezüstatomok? Útmutatás: Az időegység alatt lecsapódó részecskék számát határozzuk meg a Maxwell-eloszlás alapján, és használjuk ki az $x\sim 1/v$ összefüggést. | ||
| − | A Maxwell-féle sebességeloszlás $$F(v)=A\left(\frac{v}{v_0}\right)^3\exp{-(\frac{v}{v_0}\right)^3}.$$ | + | A Maxwell-féle sebességeloszlás $$F(v)=A\left(\frac{v}{v_0}\right)^3\exp{-\left(\frac{v}{v_0}\right)^3}.$$ |
| − | + | Az eloszlásfüggvény matematikai konstrukció, a gázmolekulák $[v,v+\mathrm{d}v)$ sebességintervallumba eső hányadát $F(v)\mathrm{d}v$ adja, a feladatmegoldás során ezzel kell számolnunk, mivel a átparaméterezéssel az infinitezimális intervallum hossza is változik. Az $[x,\mathrm{d}x]$ intervallumba érkező ezüstatomok $g(x)\mathrm{d}x$ száma megadható a részecskeáramsűrűséggel: | |
$$J_v\mathrm{d}v=g(x)\mathrm{d}x$$ | $$J_v\mathrm{d}v=g(x)\mathrm{d}x$$ | ||
| − | A $[v,v+\mathrm{d}v)$ sebességtartományban a részecskeszámokra illetve a részecskeszám-sűrűségre | + | Az ismert adatokból kifejezzül a $J_v$ részecskeáramsűrűséget. A $[v,v+\mathrm{d}v)$ sebességtartományban a részecskeszámokra illetve a részecskeszám-sűrűségre |
$$N_v\mathrm{d}v = N\,F(v)\mathrm{d}v,$$ | $$N_v\mathrm{d}v = N\,F(v)\mathrm{d}v,$$ | ||
$$n_{Vv}\mathrm{d}v = n_V\,F(v)\mathrm{d}v.$$ | $$n_{Vv}\mathrm{d}v = n_V\,F(v)\mathrm{d}v.$$ | ||
Itt a molekula-áramsűrűség definíció szerint | Itt a molekula-áramsűrűség definíció szerint | ||
$$J_v\mathrm{d}v=v n_{Vv}\mathrm{d}v$$ | $$J_v\mathrm{d}v=v n_{Vv}\mathrm{d}v$$ | ||
A lap 2012. szeptember 12., 16:41-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Kinetikus gázelmélet, transzportfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Stern híres kísérletében, amellyel a Maxwell-eloszlás kísérleti igazolását adta, 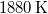 -es ezüstszálról távozó atomok sebességeloszlását mérte meg, az ábrán vázolt elrendezéssel. Az
-es ezüstszálról távozó atomok sebességeloszlását mérte meg, az ábrán vázolt elrendezéssel. Az  pontbeli tengelyen elhelyezkedő szálról távozó ezüstatomok az
pontbeli tengelyen elhelyezkedő szálról távozó ezüstatomok az  nyíláson át jutottak az
nyíláson át jutottak az  sugarú hengerfelületre. A berendezés
sugarú hengerfelületre. A berendezés  szögsebességgel forgott, aminek következtében a
szögsebességgel forgott, aminek következtében a  sebességű atom az
sebességű atom az  pont helyett
pont helyett  -ben csapódott le.
-ben csapódott le.
- a) Állapítsuk meg az
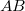 ív
ív  hosszát
hosszát 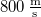 sebességű atomok esetén, ha a fordulatszám
sebességű atomok esetén, ha a fordulatszám 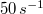 és
és 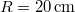 !
!
Az atomok trepülési ideje 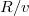 , a berendezés kerületi sebessége
, a berendezés kerületi sebessége 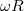 , ezzel az
, ezzel az 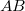 ív hossza
ív hossza
![\[x=\frac{\omega R^2}{v}.\]](/images/math/f/2/a/f2a6496a7ac4edb8c929eb7ef90f4df0.png)
- b) Milyen sebességnél adják a legnagyobb rétegvastagságot a külső hengerfelületen lecsapódó ezüstatomok? Útmutatás: Az időegység alatt lecsapódó részecskék számát határozzuk meg a Maxwell-eloszlás alapján, és használjuk ki az
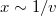 összefüggést.
összefüggést.
![\[F(v)=A\left(\frac{v}{v_0}\right)^3\exp{-\left(\frac{v}{v_0}\right)^3}.\]](/images/math/0/c/4/0c4a5cfb601aada0548d6b51a2fd867f.png)
Az eloszlásfüggvény matematikai konstrukció, a gázmolekulák 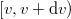 sebességintervallumba eső hányadát
sebességintervallumba eső hányadát 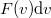 adja, a feladatmegoldás során ezzel kell számolnunk, mivel a átparaméterezéssel az infinitezimális intervallum hossza is változik. Az
adja, a feladatmegoldás során ezzel kell számolnunk, mivel a átparaméterezéssel az infinitezimális intervallum hossza is változik. Az ![\setbox0\hbox{$[x,\mathrm{d}x]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/c/a/c/cacb252b94ce8de33decf3af07b5cda7.png) intervallumba érkező ezüstatomok
intervallumba érkező ezüstatomok 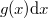 száma megadható a részecskeáramsűrűséggel:
száma megadható a részecskeáramsűrűséggel:
![\[J_v\mathrm{d}v=g(x)\mathrm{d}x\]](/images/math/e/d/1/ed1839a3e23ecef35539453f27e35496.png)
Az ismert adatokból kifejezzül a 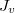 részecskeáramsűrűséget. A
részecskeáramsűrűséget. A 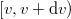 sebességtartományban a részecskeszámokra illetve a részecskeszám-sűrűségre
sebességtartományban a részecskeszámokra illetve a részecskeszám-sűrűségre
![\[N_v\mathrm{d}v = N\,F(v)\mathrm{d}v,\]](/images/math/c/1/9/c19266fd8a7556f82426d530dd9bb374.png)
![\[n_{Vv}\mathrm{d}v = n_V\,F(v)\mathrm{d}v.\]](/images/math/d/e/d/ded68dfa23b8cfc8bf27636792a55d74.png)
Itt a molekula-áramsűrűség definíció szerint
![\[J_v\mathrm{d}v=v n_{Vv}\mathrm{d}v\]](/images/math/2/9/4/294abddd44cde7af0212277a5509970a.png)